 线性代数
线性代数
# 矢量与矢量运算
# 什么是矢量和N维矢量
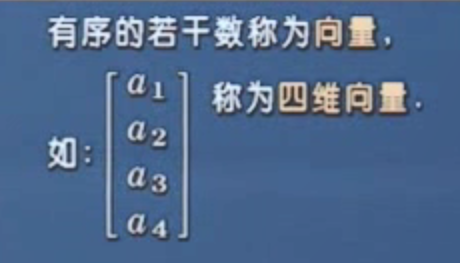
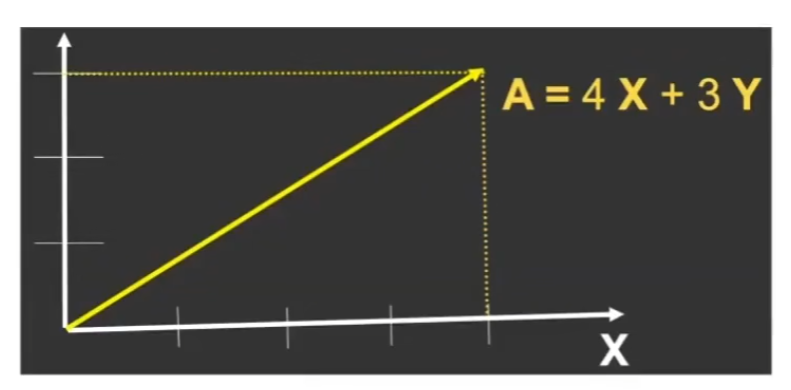
行列式和矩阵的基本构成单元是一行一行或一列一列排好次序的若干个数(向量)。有序的N个数放在一起就是N维向量。
向量并不关心它的绝对位置。
# 什么是向量的线性组合



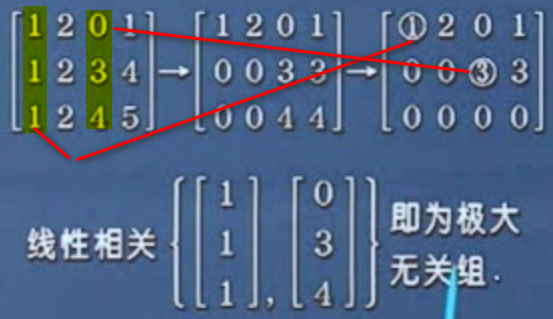
# 什么是极大线性无关组

极大线性无关组不一定是唯一的,但是极大线性无关组中向量的个数是一定的。向量组的秩等于极限线性无关组中向量的个数。(有几个无关的向量,它的秩就是这个无关向量的数)


# 点和矢量的区别是什么
- 点表示的是坐标空间中的一个位置。
- 矢量表示的是一个点在某个方向上相对另一个点的位置,是个相对位移量,点可以看作是相对于坐标系原点的一个矢量。
# 矢量运算有哪些
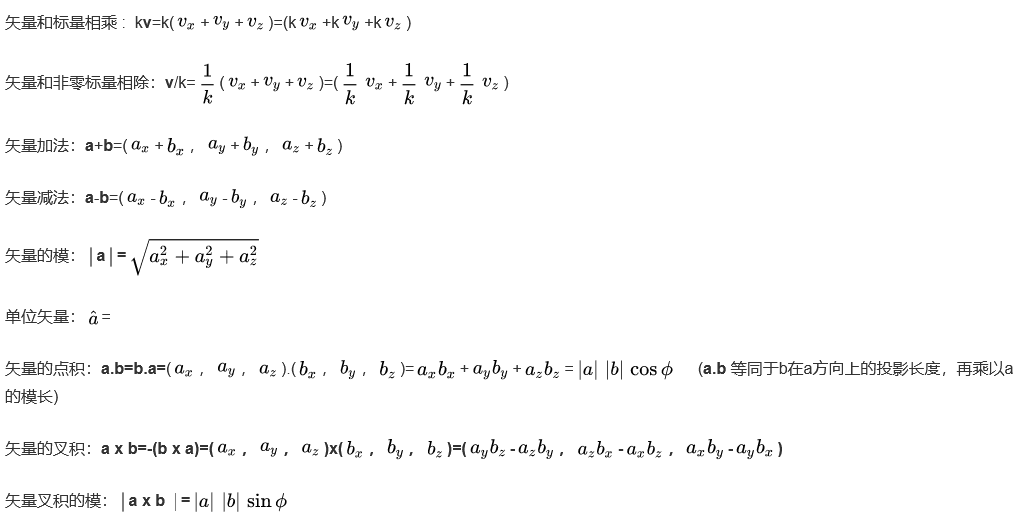
# 什么是矢量的归一化(单位向量)
单位矢量指的是模为1的矢量,单位矢量也称为归一化矢量。
向量除以它的模后就是单位向量。
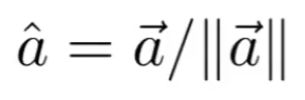
# 向量加(减)法

向量求和有平行四边形法则 和 三角形法则两种表示方法
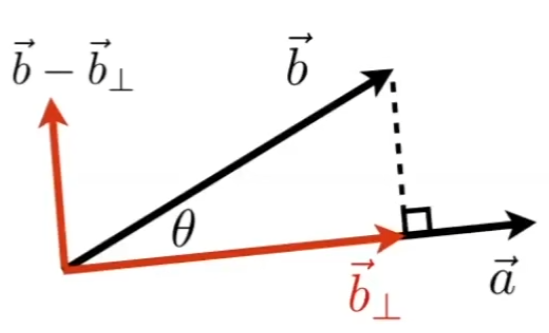
# 矢量点积(内积)及其几何意义
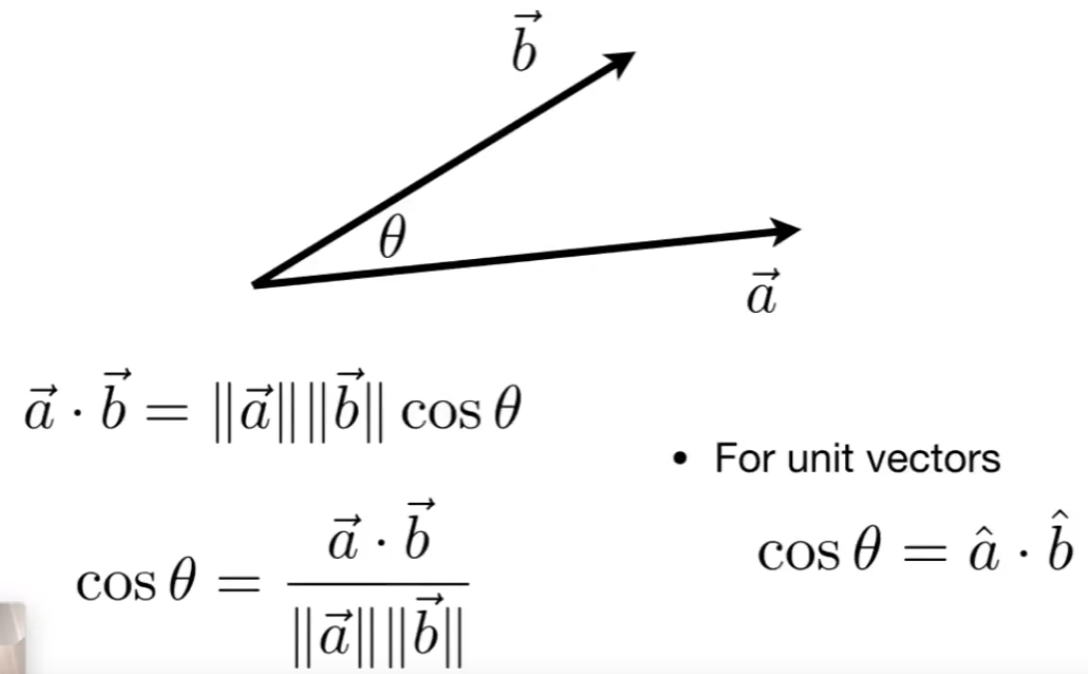
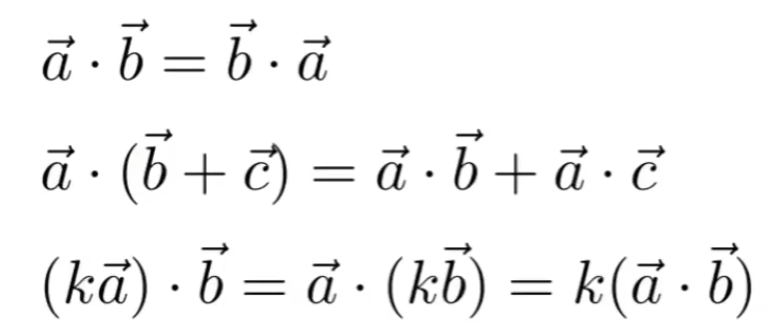
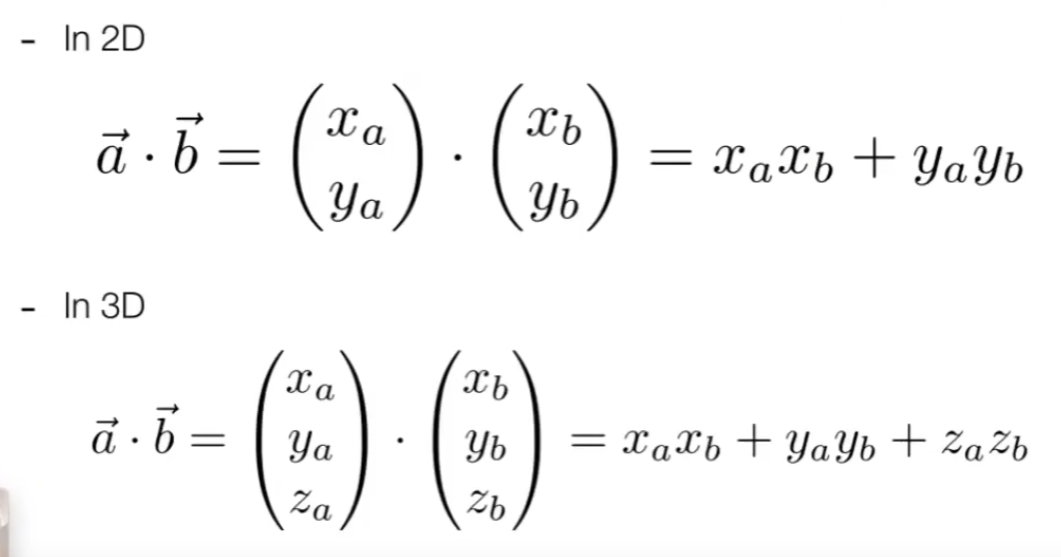
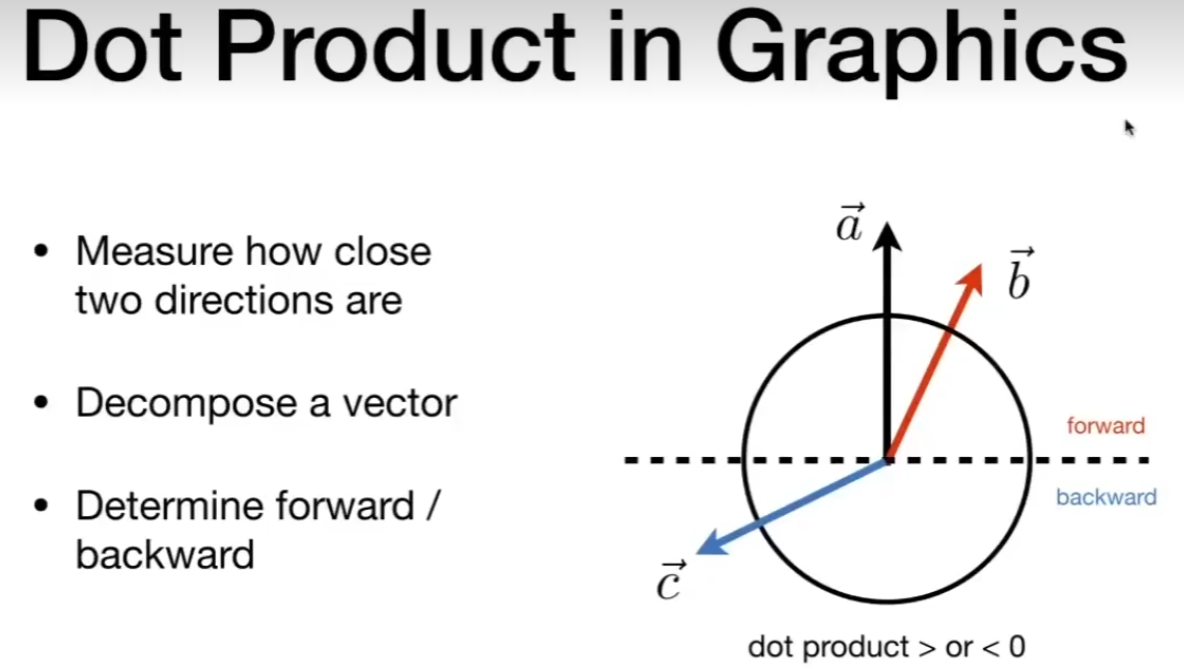
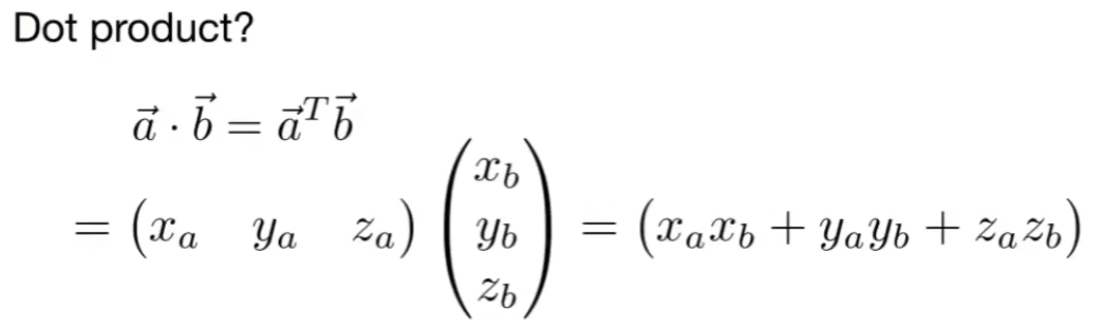
向量点乘的几何意义:一个向量在另一个向量上的投影。
# 矢量叉积(外积)及其几何意义
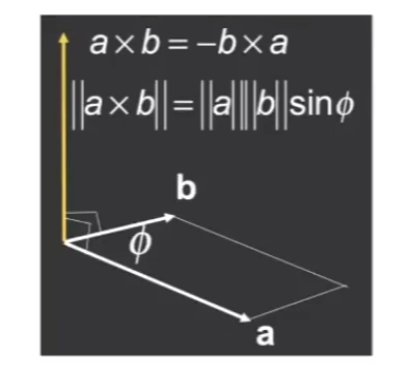


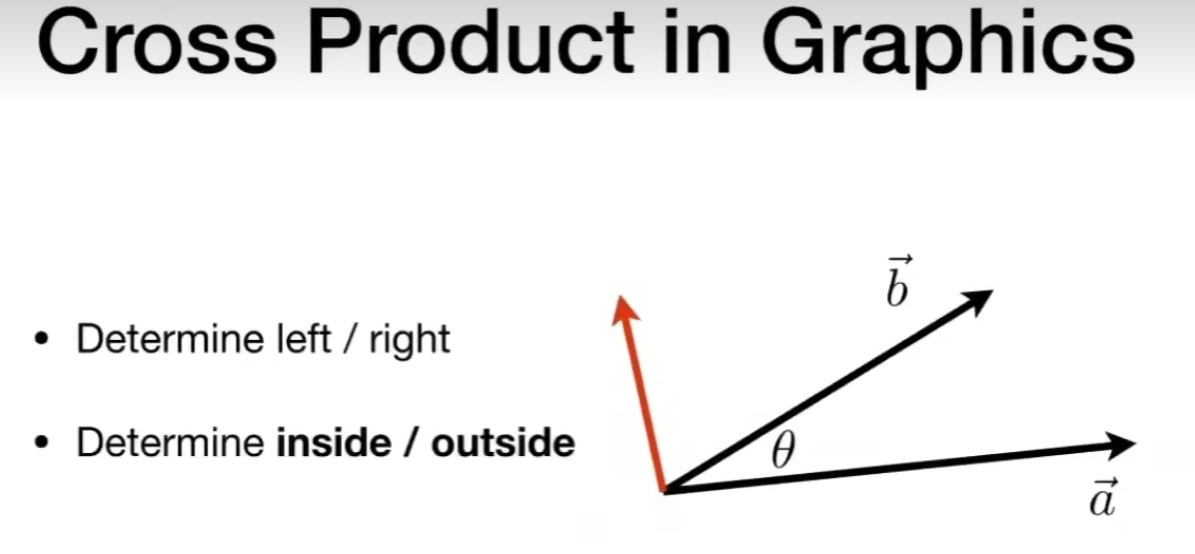

向量叉乘在图形学中可以判定左和右。还可以判定内和外。
向量叉乘几何意义:两个向量所构成平面的方向向量。要注意使用的是左手还是右手坐标系,方向受此影响。
# 矢量和标量相乘的几何意义
将一个矢量放大n倍。
# 矩阵与矩阵运算
# 什么是矩阵
矩阵就是一个表格(比喻的方式理解)。矩阵的行列数可以不相同。
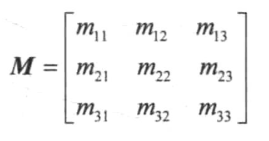
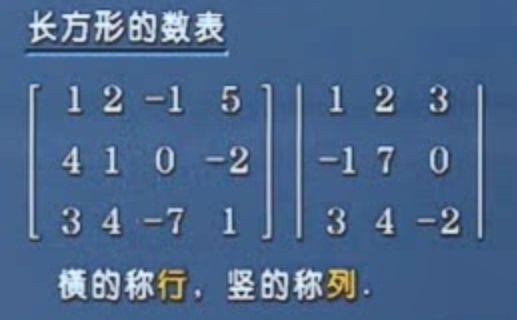
# 什么是矩阵的秩
秩是矩阵的一个特征。矩阵中非零子式的最高阶数称为矩阵的秩。

# 什么是阶梯阵
下图所示的矩阵就是一个阶梯阵,阶梯阵的秩等于非零行的行数。

# 矩阵相等

# 矩阵和标量相乘
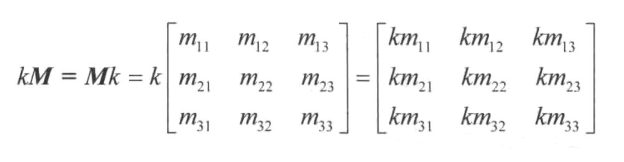
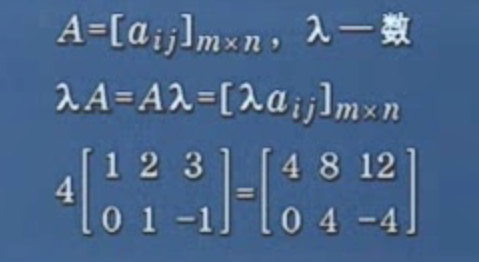
# 矩阵运算和数运算不同之处

# 矩阵相加

# 减法类似加法
略
# 除法类似乘法
略
# 矩阵与矩阵相乘的条件
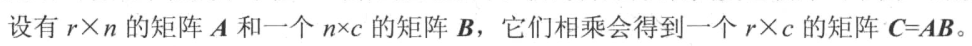


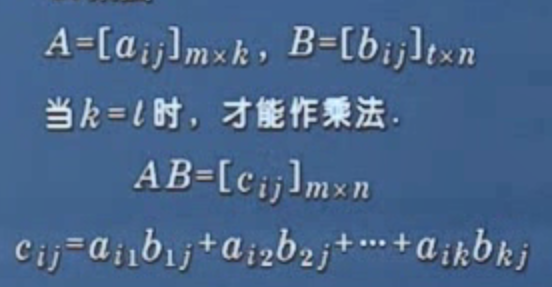

# 矩阵乘法不满足交换律,但满足结合律
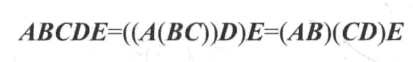

# 方块矩阵及其特性
方块矩阵简称方阵,是指那些行数和列数相同的矩阵。方阵的对角元素是指行数和列数相等的元素,一般在方阵的对角线上。
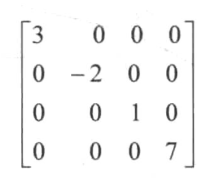
# 对角矩阵
如果一个矩阵除了对角元素外都为0,那么这个矩阵就叫做对角矩阵。
# 单位矩阵
对角元素均为1的对角矩阵叫做单位矩阵。
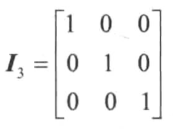
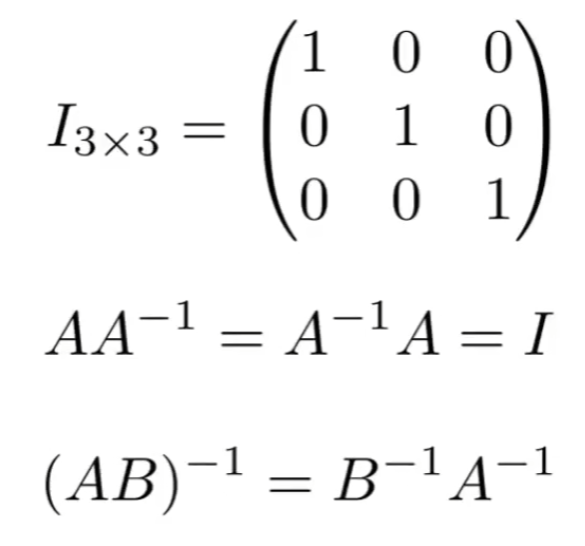
# 转置矩阵
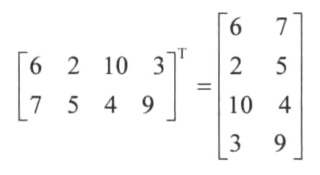
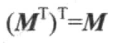
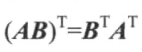


# 逆矩阵
逆矩阵首先是一个方阵。但并非所有的方阵都有逆矩阵。如果一个矩阵的行列式不为0,那么这个矩阵就是可逆矩阵。
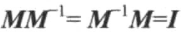
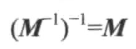
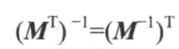


# 正交矩阵
如果一个方阵和它的转置矩阵相乘为单位矩阵的话,那么这个矩阵就是正交矩阵。
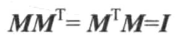
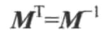
# 矩阵的特征值和特征向量

# 矩阵特征值和特征向量的求法


# 什么是相似矩阵



对称阵一定是可以对角化的。
# 行列式
# 行列式以及如何计算行列式
数学是研究数量的科学,可分为三种:连续量、离散量和随机量。微积分、线性代数和概率论与数理统计分别是研究这三种量的最基础的课程。计算机科学研究离散量。其中行列式是线性代数中研究的一个工具,行列式的行数和列数一定是相同的,行列式表示的是其元素之间一种特定的运算。如下所示:
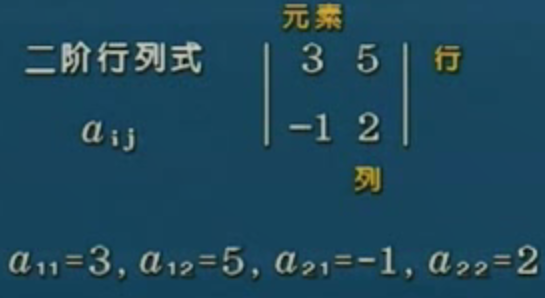
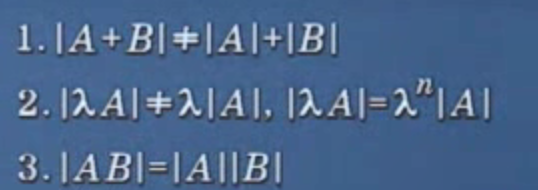
# 行列式展开
行列式的值等于按任何一行(列)展开。某一行某一列所有元素*代数余子式的和。

# 什么是行列式某一元素的余子式?什么是代数余子式
把行列式某个元素所在的行列去掉,剩下的就是行列式某个元素的余子式。如下所示:

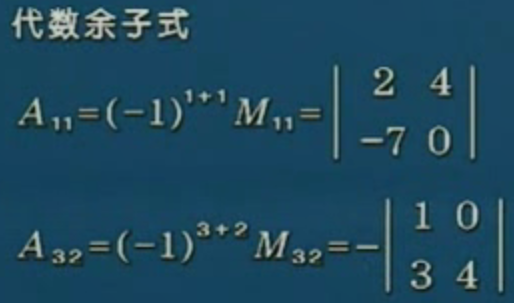
# 行列式的性质
- 行、列交换,其值不变。
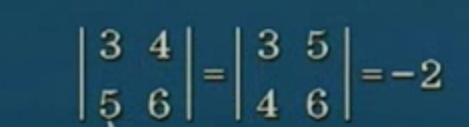
- 两行交换,其值变号。
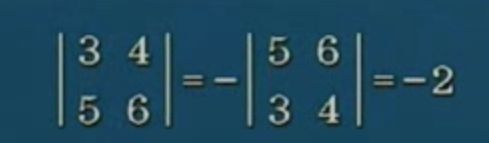
- 某一个行有公因子,可以提出该公因子。
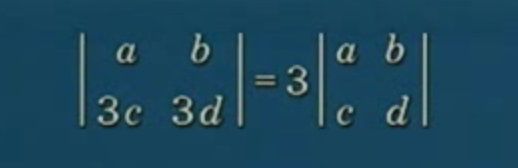
- 对行的倍加运算,其值不变
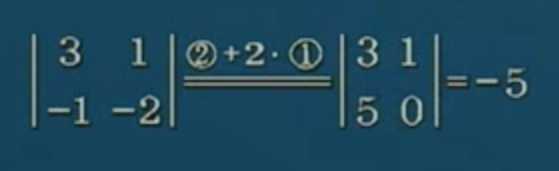
行列式与它的转置行列式相等。
行列式有两行成比例,则该行列式的值为零。
# 什么是初等行变换
- 两行交换
- 某一行乘以非零常数
- 某一行乘以一个常数加到另一行
- 初等行变换是不会改变秩的变换

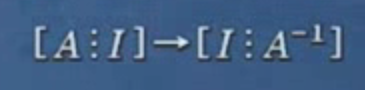

# 什么是线性方程组?表达?解法?理论?

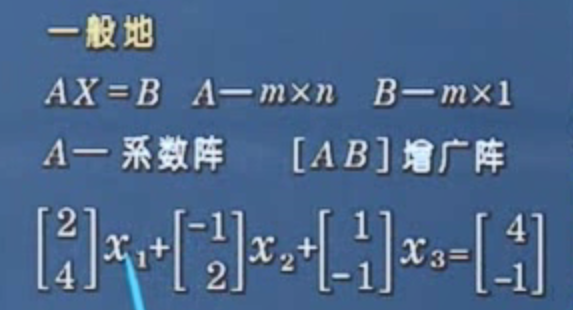
线性方程组理论有3个核心问题:是否有解;若有解,解是否唯一;若不唯一,如何掌握其全体。






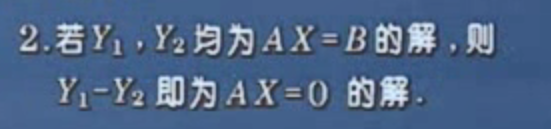
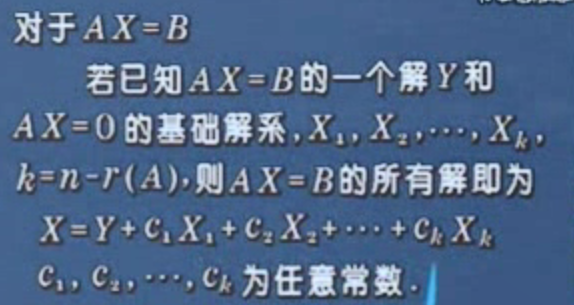

# 二次型及其表示?标准型?正定二次型?

