关于概率论与数理统计

研究对象

• 确定现象：必然发生或者不发生。
• 随机现象：个别试验结果呈现不确定性，大量随机试验结果呈现统计规律性。

概率论与数理统计是研究和揭示随机现象统计规律性的学科。概率论是数学的一个分支，研究如何定量描述随机现象及其规律。数理统计则是以数据为唯一研究对象，包括数据的收集、整理、分析和建模，从而对随机现象的某些规律进行预测或决策。大数据时代的来临，更为统计学的发展带来了极大的机遇和挑战。

如何学习这门课程

学好概率论的关键是要抓住随机和数据这两个关键方面。

• 学思想：概率统计特殊的研究对象包含了许多独特的思维方式和思想方法，特别是如何看待和处理随机规律性，是其他学科中没有的。
• 学方法：定量描述随机现象及其规律的方法，收集、整理、分析数据，从而建立统计模型的方法。
• 学应用：尽可能多地了解各种概念的背景、各种方法和模型的实际应用。不仅要学课程中提及的，也要自己收集、寻找各种实例。
• 学软件：数据处理的最后结果必须通过计算机实现。应该掌握统计软件的使用和结果分析。

概率论的基本概念

• 随机试验：既包括科学试验，也包括对某一事物的某一特征的观察。
• 确定现象：也叫必然性现象，是指在一定条件下必然发生的现象。
• 随机现象：也叫偶然性现象，是指在一定条件下具有多种可能结果，且试验时无法预知出现哪个结果的现象，也就是可能发生也可能不发生的现象。
• 试验：观察、测量统称为试验。
• 随机试验：用 E 表示，有三个特征。1 在相同的情况下可以重复。 2 结果不止一个，结果无法预测。 3 可能出现的结果总数是明确的。
• 随机试验的结果叫事件，随机事件简称事件。
• 基本事件是指相对于试验目的不能再分的事件。
• 复合事件是指由基本事件复合而成的事件。
• 必然事件是指每次试验一定发生的事件。
• 不可能事件是指每次试验一定不发生的事件。
• 样本空间是指所有基本事件的集合。
• 样本点是指样本空间中的元素。
• 无限可列个是指按某种规律排成一个序列。
• 互不相容事件是指不能同时发生的事件。
• 对立事件是指互不相容的事件并且它们的并集是整个样本空间。
• 完备事件组是指所有事件两两互不相容并且它们的并集是整个样本空间。

随机事件及其运算

随机试验

随机现象在一次试验中呈现不确定的结果，而在大量重复试验中结果将呈现某种规律性。例如相对比较稳定的性别比例，这种规律性称为统计规律性。为了研究随机现象的统计规律性，就要对客观事物进行观察，观察的过程叫随机试验，简称试验，记为E。

随机试验有以下三个特点：

1. 在相同的条件下试验可以重复进行；
2. 每次试验的结果不止一种，但是试验之前必须明确试验的所有可能结果；
3. 每次试验将会出现什么样的结果是事先无法预知的。

举个随机试验的栗子

1. 抛一枚硬币，观察正面H(Head)、反面T(Tail)出现的情况。
2. 将一枚硬币抛掷三次，观察正面H、反面T出现的情况。
3. 将一枚硬币抛掷三次，观察出现正面H的次数。

样本空间

随机试验的一切可能结果组成的集合称为样本空间，记为Ω={ω}或S={e}，其中ω表示试验的每一个可能结果，又称为样本点，即样本空间为全体样本点的集合。

注释

样本空间S：Sample的简写。样本点e：Element的简写。

举个样本空间栗子

• 抛掷一枚均匀硬币的样本空间为Ω={H，T}，其中H表示正面朝上，T表示反面朝上；
• 抛掷一枚均匀骰子的样本空间为Ω={1，2，…，6}；
• 某快餐店一天内接到的订单量的样本空间为Ω={0，1，2，…，n，…}；
• 某航班起飞延误时间的样本空间为Ω={t：t≥0}；
• 一支正常交易的A股股票每天涨跌幅的样本空间为Ω={x：-10%≤x%≤10%}。

小结

• 从上面的例子中可以看出，样本空间中的元素可以是数，也可以不是数。
• 从样本空间中含有样本点的个数来看，可以是有限个也可以是无限个；可以是可列个也可以是不可列个。
• 样本空间的求法有列举法(有限个)和描述法(无穷个)。

随机事件

当我们通过随机试验来研究随机现象时，每一次试验都只能出现Ω中的某一个结果ω，各个可能结果ω是否在一次试验中出现是随机的。在随机试验中，常常会关心其中某一些满足某种条件的结果是否出现。例如，抛掷一枚均匀的骰子，关心掷出的点数是否是奇数；航班起飞关心延误时间是否超过3个小时等。这些在一次试验中可能出现，也可能不出现的一类结果称为随机事件，简称为事件，随机事件通常用大写字母A，B，C，…表示。

从集合的角度来说，样本空间的部分样本点组成的集合称为随机事件。样本空间包含所有样本点，在每次试验中它总发生，其构成的事件称为必然事件。如果事件只包含一个样本点，称为基本事件。如果事件不包含任何样本点，那么这个事件是空集，每次试验空集都不发生，称为不可能事件。在每次试验中，当且仅当随机事件中的一个样本点出现，称为事件发生。

小结

• 必然事件S，每次E中均发生的事件。样本空间S也是自己的一个子集，所以它也称为一个事件。由于Ω包含所有可能的试验结果，所以S在每一次试验中一定发生，又称为必然事件。
• 不可能事件∅，每次E中都不发生的事件。空集∅也是样本空间S的一个子集，所以它也称为一个事件。由于∅中不包含任何元素，所以∅在每一次试验中一定不发生，又称为不可能事件。
• 随机事件A，除了上面两种情况外的其他事件。

抛掷一枚均匀的骰子的样本空间为Ω={1，2，…，6}

• 随机事件A=“出现6点”={6}；
• 随机事件B=“出现偶数点”={2，4，6}；
• 随机事件C=“出现的点数不超过6”={1，2，…，6}=Ω，即一定会发生的必然事件；
• 随机事件D=“出现的点数超过6”=∅，即一定不会发生的不可能事件。

事件间的关系

随机事件的关系可以按照集合之间的关系来处理，假设给定一个随机试验，Ω是它的样本空间，A，B，C，…都为Ω的子集，则随机事件间的关系有以下几种

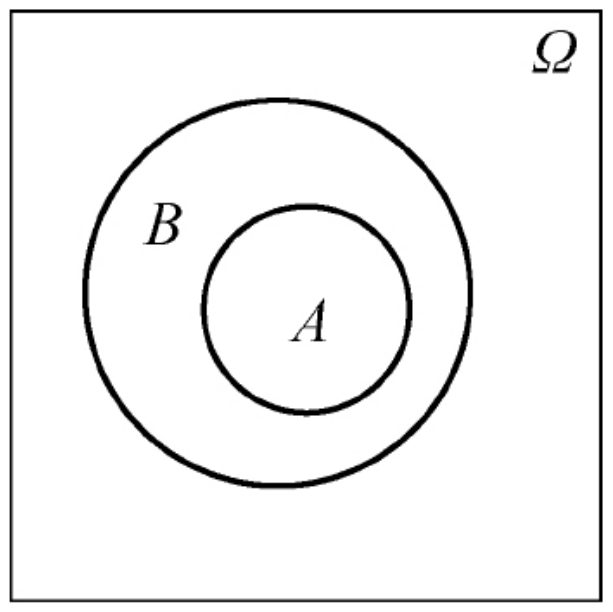
• 包含关系：如果A⊂B（或B⊃A），则称事件A包含在B中（或称B包含A）。从概率论的角度来说：事件A发生必然导致事件B发生。
• 相等关系：如果A⊂B，B⊂A同时成立，则称事件A与B相等，记为A=B。从概率论的角度来说：事件A发生必然导致事件B发生，且B发生必然导致A发生，即A与B是同一个事件。
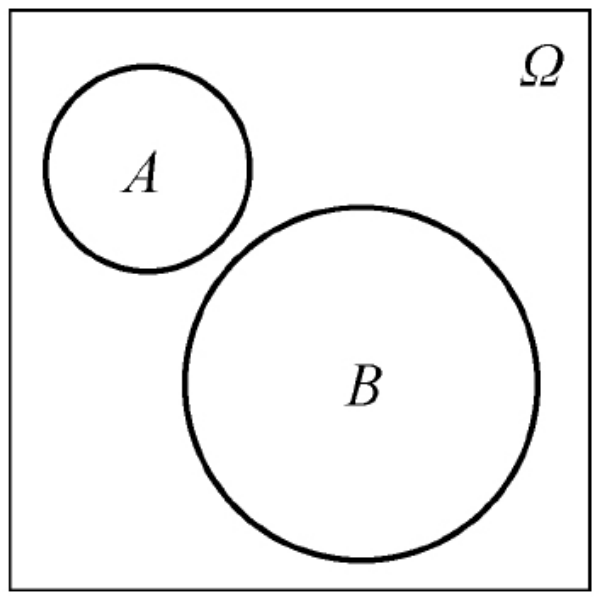
• 互斥关系：如果A与B没有相同的样本点，记作AB=∅，则称事件A与B互不相容（或称为互斥）。从概率论的角度来说：事件A与事件B不可能同时发生。
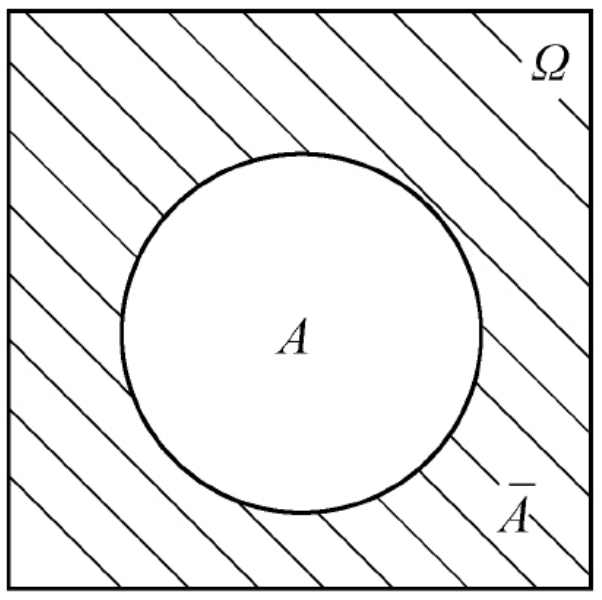
• 对立关系：如果A与B没有相同的样本点，并且A和B构成了整个样本空间，记作AB=∅且A∪B=Ω。在一次试验中，事件A和B有且只有一个发生。

事件间的运算

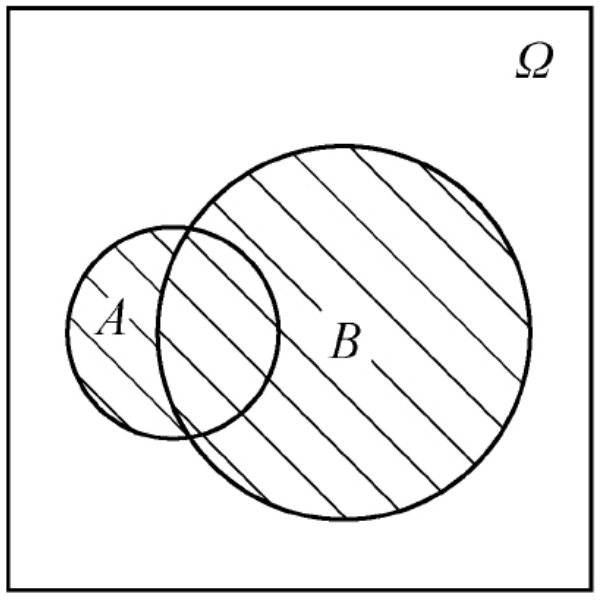
与集合的运算一样，随机事件的运算也有并、交、差

• 事件A与B的并，记为A∪B，从概率论的角度来说：事件A与B中至少有一个发生。
• 事件A与B的交，记为A∩B（或AB），从概率论的角度来说：事件A与B同时发生。
• 事件A与B的差，记为A-B，从概率论的角度来说：事件A发生且B不发生。

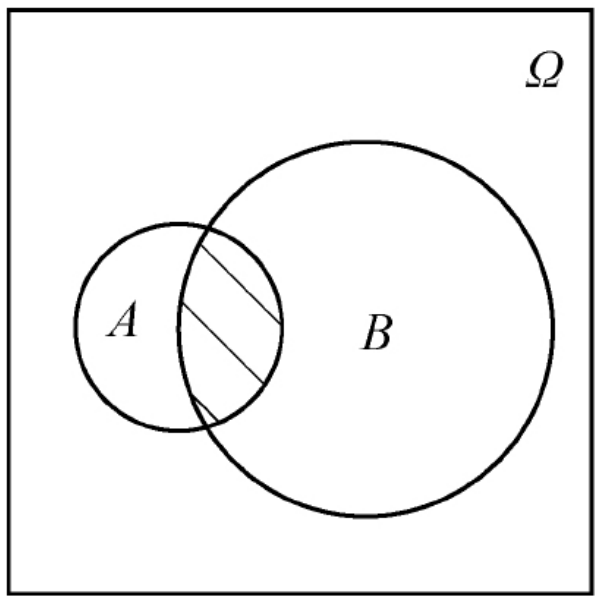
事件的运算性质，如集合的运算性质一样满足下述定律

概率的定义及其性质

• 概率的描述性定义：随机事件A发生的可能性大小的度量(非负值)为事件A发生的概率。

• 概率的统计性定义：也叫频率，是在相同条件下，进行了n次试验，在这n次试验中，事件A发生的次数na，称为事件A发生的频率，比值na/n称为事件A发生的频率，并记作fn(A)。或者定义为随着试验次数n的增大，频率值逐步"稳定"到一个实数，这个实数称为事件A发生的概率。

  频率的基本性质

  频率试验

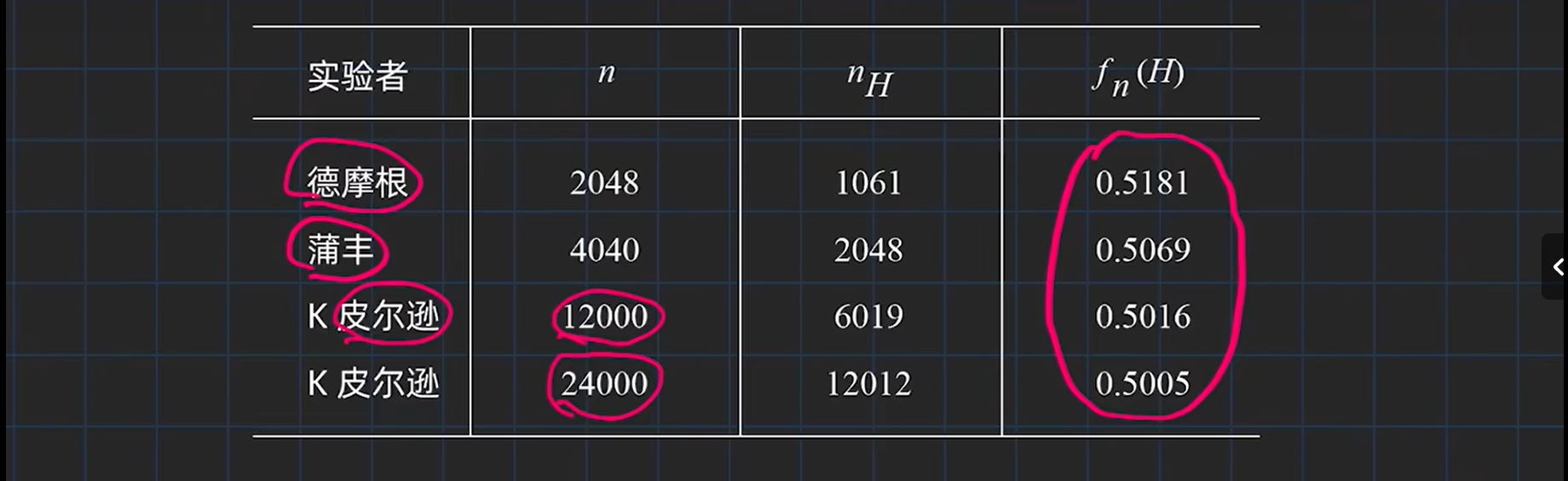
• 概率的公理化定义：设任一随机试验E，Ω为相应的样本空间，若对任意事件A，有唯一实数P（A）与之对应，且满足下面条件，则数P（A）称为事件A的概率：

  1. 非负性公理　对于任意事件A，总有P（A）≥0；
  2. 规范性公理 P（Ω）=1；
  3. 可列可加性公理　若A1，A2，…，An为两两互不相容的事件，则有
  

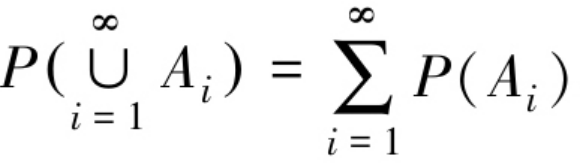
  概率的重要性质 性质1：P（∅）=0；性质2：有限可加性；性质3：减法公式；性质4：单调性；性质5：有界性；性质6：逆事件概率；性质7：加法公式。

等可能概型

在概率论发展的历史上，最先研究的是一类最直观、最简单的随机现象。在这类随机现象中，样本空间中的每个基本事件发生的可能性都相等，这样的数学模型我们称之为等可能概型。其中，当样本空间只包含有限个不同的可能结果（即样本点），如抛掷一枚均匀的硬币、抛掷一枚均匀的骰子等，研究这一类随机现象的数学模型我们称之为古典概型。而当样本空间是某个区域（可以是一维区间、二维平面或三维空间），如搭乘地铁等待时间、蒲丰投针问题等，研究这一类随机现象的数学模型我们称之为几何概型。

基本原理

• 加法原理：完成一件事，可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1+m2+…+mn种不同方法。
• 乘法原理：完成一件事，需要分成n个步骤，做第一步时有m1种不同的方法，做第二步时有m2种不同的方法，……，做第n步有mn种不同的方法，那么完成这件事共有N=m1m2…mn种不同的方法。
• 不可重复排列：从n个不同的元素中任取r（1≤r≤n）个不同元素，按一定的顺序排成一列，称之为排列。A(n, r)=n!/(n-r)! 其中，n 表示总数，r 表示选取的项目数。
• 可重复排列：从n个不同元素中，每次可以重复地取出m个元素排成一列，所有这样排列的个数称为从n个不同元素中取出m个元素的元素可重复排列数。
• 组合：从n个不同的元素中任取r（1≤r≤n）个不同元素，不考虑次序将它们并成一组，称之为组合。C(n, r) = n! / (r! * (n - r)!) 其中，n 表示总数，r 表示选取的项目数。

古典概型

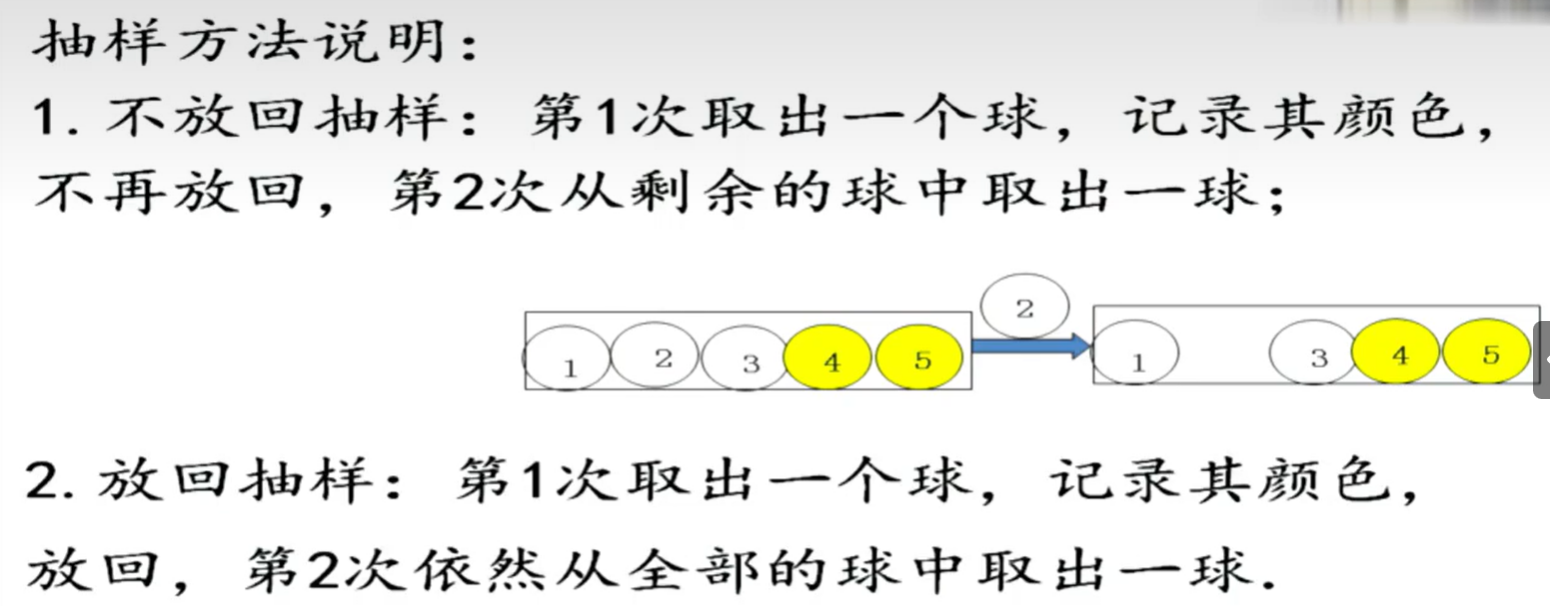
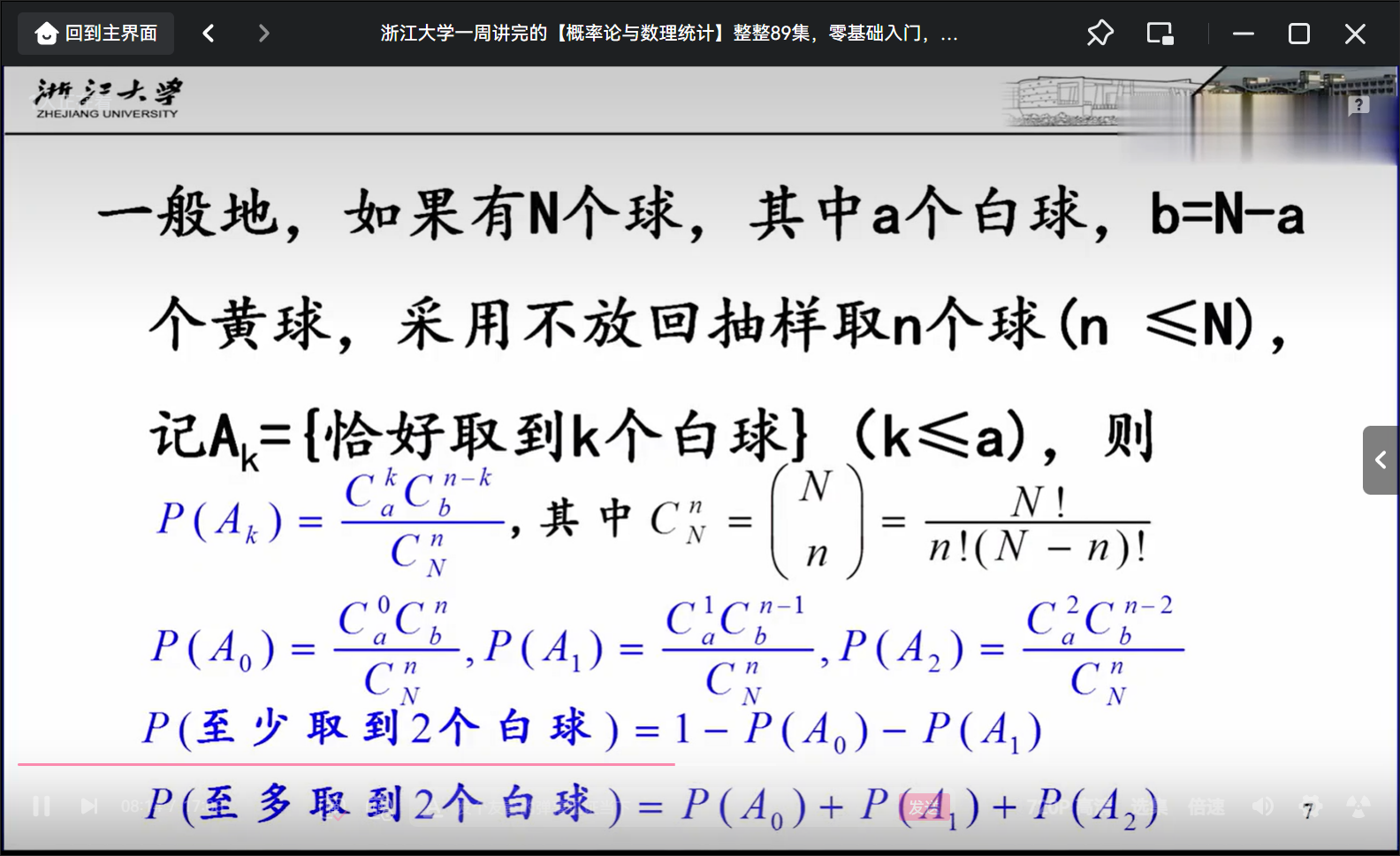
几何概型

举个几何概型的栗子

小结

1. 古典概型：基本事件有限、等可能的随机试验；几何概型：基本事件无限、等可能的随机试验；
2. 求几何概型，关键是画出区域，并求其度量。

条件概率与事件的相互独立性

条件概率

条件概率是概率论中一个既重要又应用广泛的概念．例如，在购买人寿保险时，不同年龄的投保人的保费是不同的，那是因为不同年龄的投保人在未来一年内死亡的概率是有差异的。一般地，条件概率是指在某随机事件A发生的条件下，另一随机事件B发生的概率，记为P（B|A），它与P（B）是不同的两类概率。

条件概率的定义：

条件概率的性质：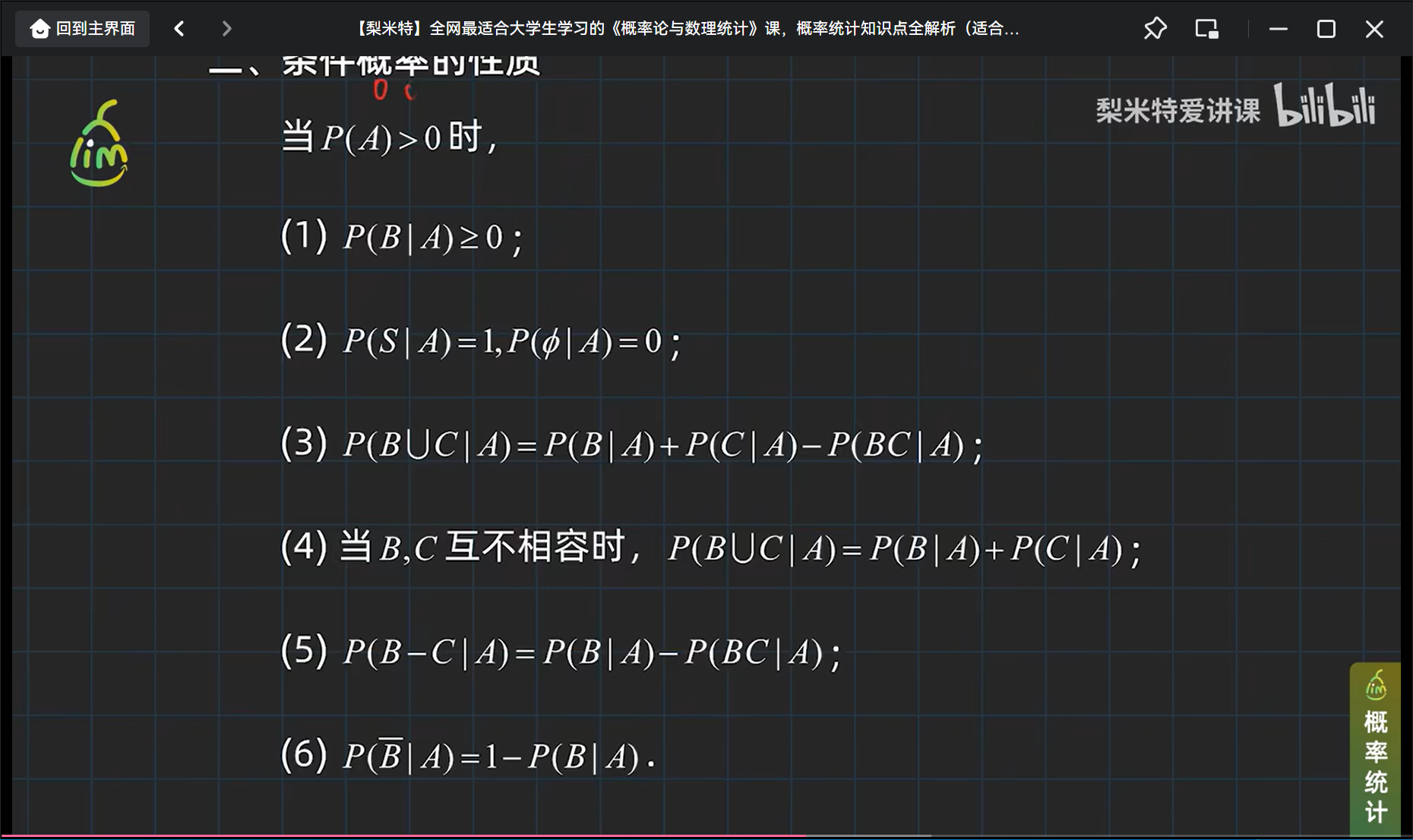

举个条件概率的栗子

乘法定理(乘法公式)

事件的相互独立性

一般来说，设A，B为试验E的两个事件，且P（A）>0，则事件A的发生对事件B发生的概率是有影响的，这时条件概率P（B|A）≠P（B）；但例外的情况也不在少数，这时就会有P（B|A）=P（B），则可以推出P（AB）=P（A）P（B|A）=P（A）P（B）。

定义2　设A，B为试验E的两个事件，如果满足等式P（AB）=P（A）P（B），则称事件A，B相互独立，简称A，B独立。

定义3　设A，B，C是试验E的三个事件，如果满足等式P（AB）=P（A）P（B），P（AC）=P（A）P（C），P（BC）=P（B）P（C）。则称事件A，B，C两两相互独立。

全概率公式与贝叶斯公式

全概率公式是概率论中一个非常重要的公式。通常我们会遇到一些较为复杂的随机事件的概率计算问题，这时，如果将它分解成一些较容易计算的情况分别进行考虑，可以化繁为简。

定义：设E是随机试验，Ω是相应的样本空间，A1，A2，…，An为Ω的一个事件组，若满足条件：（1）Ai∩Aj=∅（i≠j）；（2）A1∪A2∪…∪An=Ω。则称事件组A1，A2，…，An为样本空间的一个完备事件组，完备事件组完成了对样本空间的一个分割。

贝叶斯公式

贝叶斯公式是概率论中最重要的知识点之一，该公式的意义在于开创了统计学的一个学派——贝叶斯学派，它和经典统计学学派为现代统计学的两大分支。贝叶斯公式是由英国学者贝叶斯（Thomas Bayes，1701年—1761年）为了解决二项分布的概率估计问题所提出的一种“逆概率”思想发展而来的。“求概率这个问题的逆概率”是指已知事件的概率为p，可计算某种结果出现的概率问题；反之，给定了观察结果，则可对概率p作出试验后的推断。即“正概率”是由原因推结果，“逆概率”是由结果推原因。贝叶斯的思想，以及其支持者对其思想的发展和在应用上的良好表现，最终发展成了贝叶斯统计理论，从而开辟了统计学发展中的一个新领域，对统计决策函数、统计推断、统计的估算等做出了贡献。贝叶斯学派与经典统计学的差别在于是否使用先验信息，先验信息是指人们对一个事物的历史认知或主观判断。众所周知，任何事物都是发展变化的，都会通过样本数据信息不断挖掘和发现新变化。经典统计学只使用样本数据信息，而贝叶斯分析则是把先验信息与样本数据结合起来进行推断。