 随机变量及其分布
随机变量及其分布
在上一章中,我们发现基于随机试验的样本空间去研究随机事件及其概率的过程中,有时样本空间不一定是数集,不便于用数学方法来处理。为了能进行定量的数学处理,必须要把随机试验的结果数量化。因此,通过引入随机变量,将样本空间转化为一个无量纲的数集,使得能统一地处理随机现象,而且过程会更简单直接。本章中我们将主要讨论一维随机变量及其分布。
# 随机变量及其分布
# 随机变量的定义
在实际工作中,经常见到的一类随机变量是离散型随机变量。在随机试验中有很多试验结果本身就是用数量表示。在随机试验中还有很多试验结果本身不是用数量表示,这时可以根据需要设置变量。
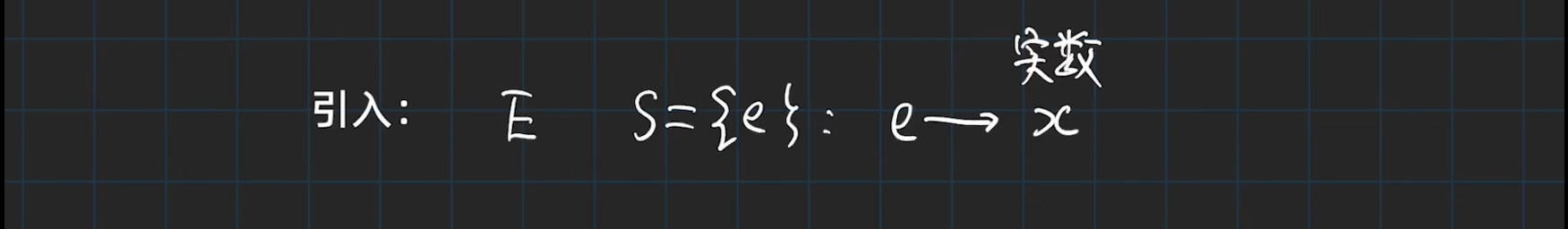
举个随机试验的结果是数量的栗子
- 抛掷一枚均匀的骰子,出现的点数X的取值;
- 每年每辆参保的车辆会发生理赔的次数N,每次理赔的金额Y,这里N和Y的取值;
- 测量的随机误差ε的取值。
举个随机试验结果不是数量的栗子
- 抛掷一枚均匀的硬币,观察其朝上的面,则样本空间Ω={正面朝上,反面朝上}。这时,可按如下方式设置一个变量X:在这里,X的取值对应如下随机事件:{X=1}={正面朝上},{X=0}={反面朝上} 。
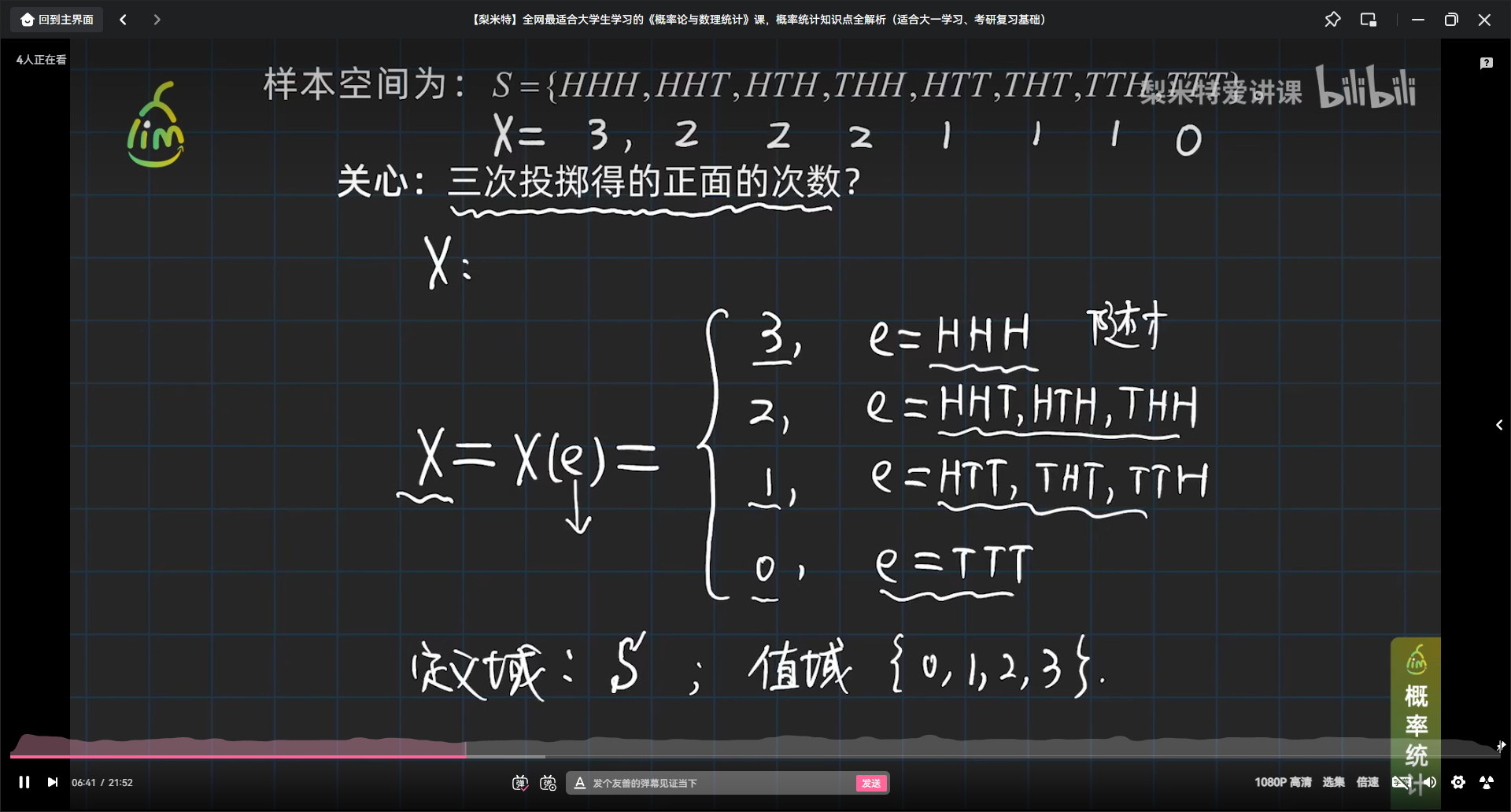
- 抛掷三枚均匀的硬币,观察其朝上的面,则样本空间Ω={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT},其中H表示正面朝上,T表示反面朝上。这时,若一个变量X表示“三次抛掷中反面朝上的次数”,则X的取值与样本点之间有如下的对应关系:在这里,X的取值对应如下随机事件:{X=0}={反面朝上0次}={HHH},{X=1}={反面朝上1次}={HHT,HTH,THH},{X=2}={反面朝上2次}={HTT,THT,TTH},{X=3}={反面朝上3次}={TTT}。
定义


提示
随机变量一般用大写字母X,Y等来表示,随机变量的取值一般用小写字母x,y等来表示。如果一个随机变量仅可能取有限或可列个值,则称其为离散型随机变量。如果一个随机变量的取值充满了数轴上的一个区间(或某几个区间的并),则称其为非离散型随机变量。连续型随机变量就是非离散型随机变量中最常见的一类随机变量。
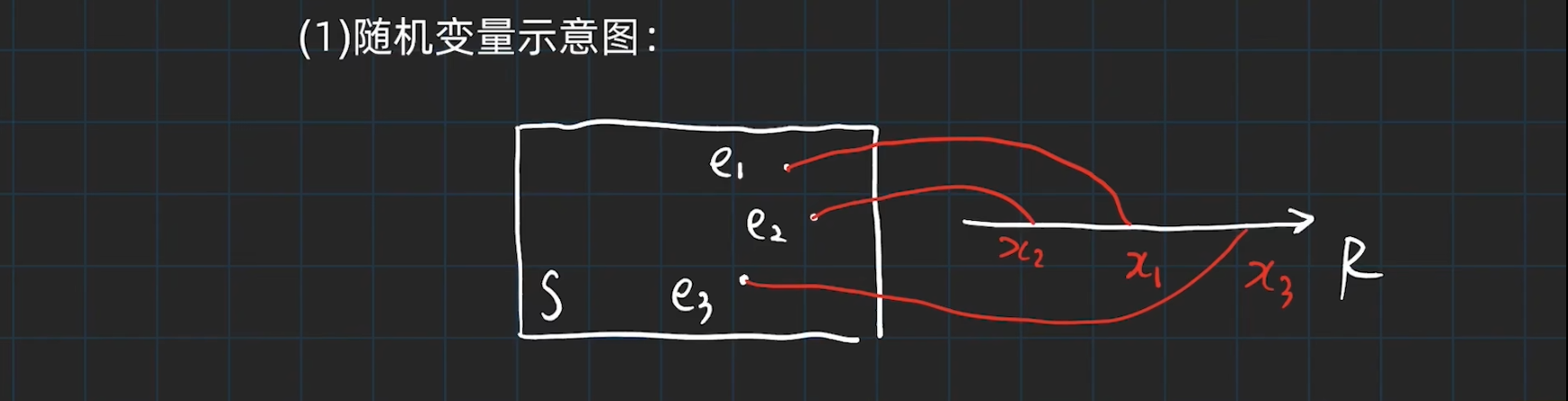
随机变量的定义可直观解释为:随机变量X是样本点的函数,这个函数的自变量是样本点,可以是数,也可以不是数,定义域是样本空间,而因变量必须是实数。这个函数可以让不同的样本点对应不同的实数,也可以让多个样本点对应于一个实数。
随机变量的引入是概率论发展走向成熟的一个标志,它弥补了随机试验下的随机事件种类繁多、不易一一总结它们发生的可能性大小的规律的缺陷,因为如果知道随机变量的分布,随机试验下任一随机事件的概率也随之可以得到;另外引入随机变量后,可以使用数学中的微积分工具讨论随机变量的分布。
# 离散型随机变量及其分布律
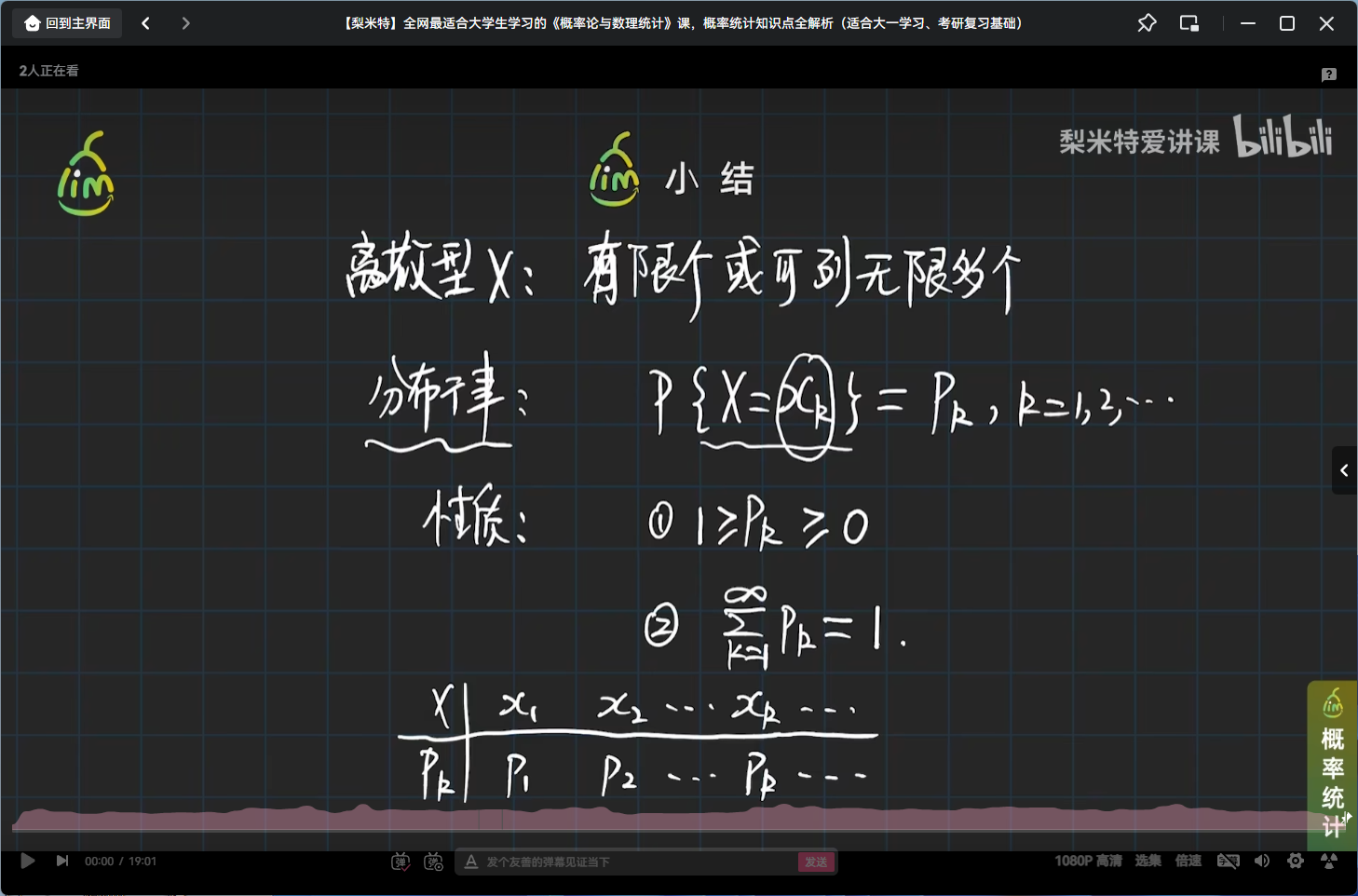
定义

性质

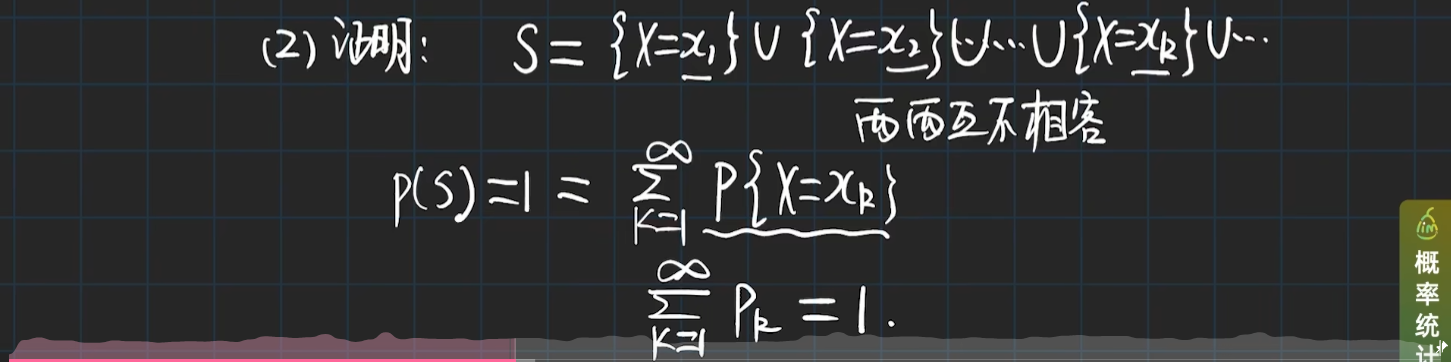
提示
从上面的分析中可以发现,分布函数和分布律对离散型随机变量的取值规律描述是等价的,比较而言,分布律更直观、方便。
举个离散型随机变量分布律的栗子
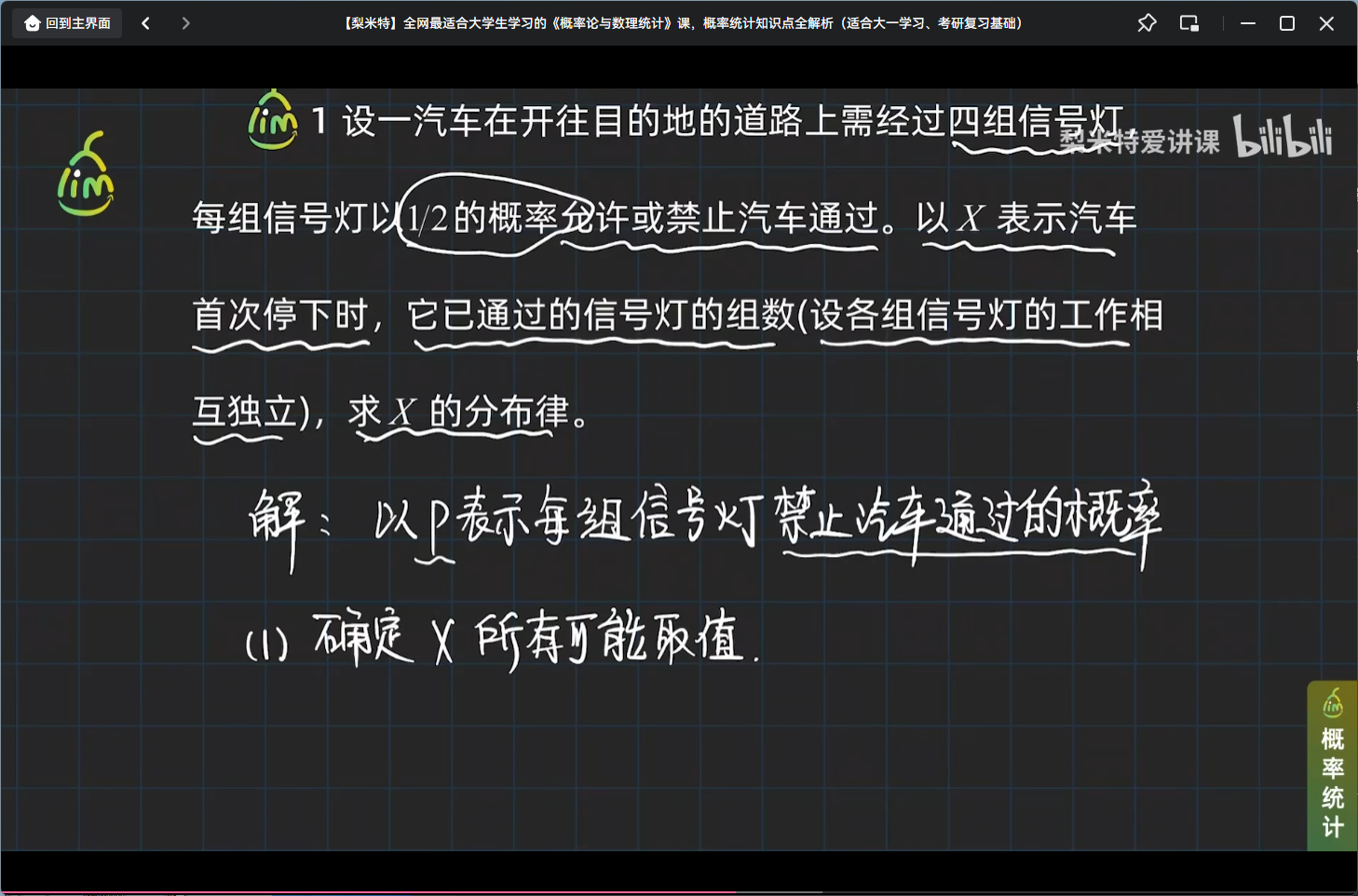

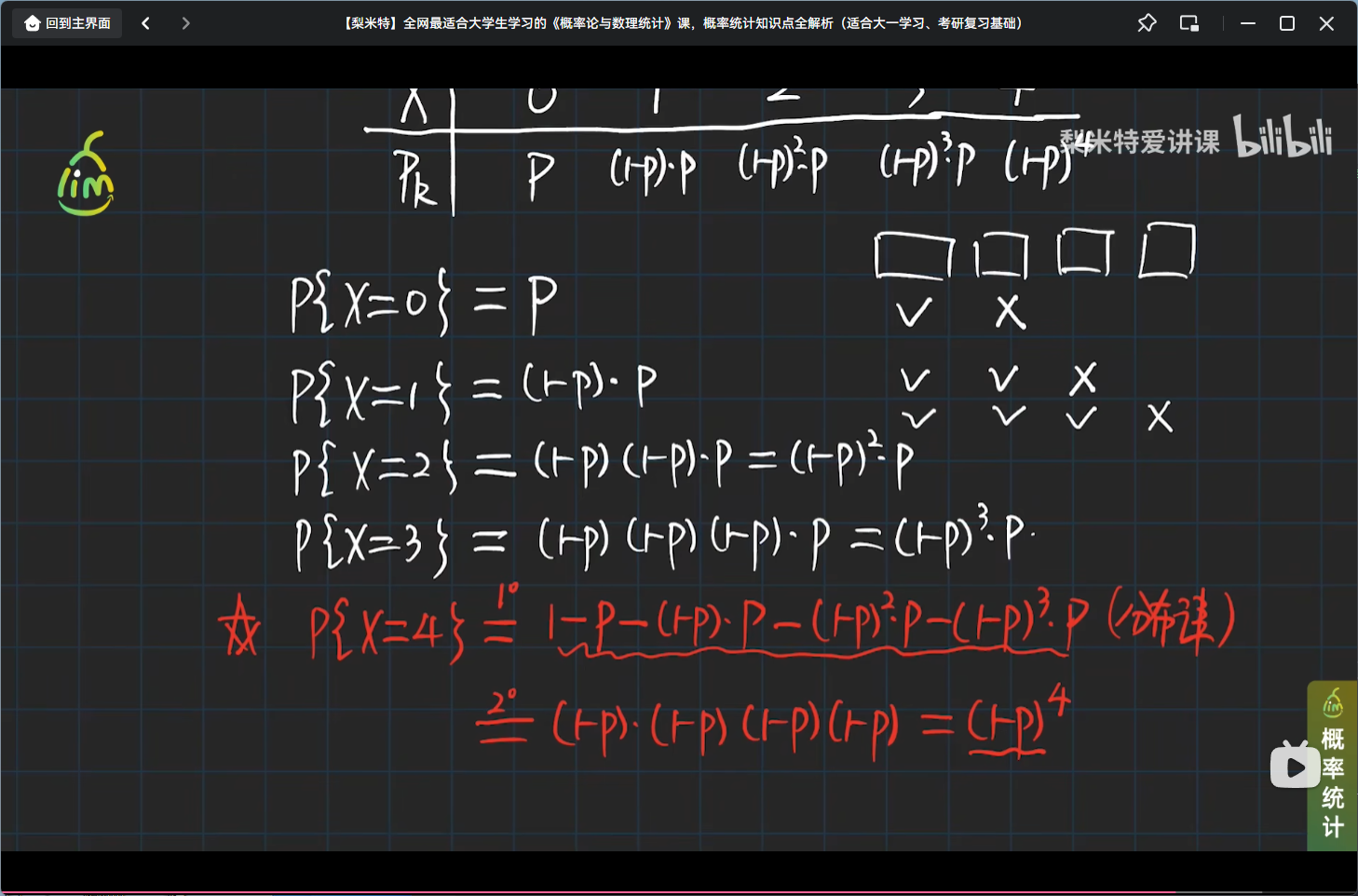
小结
# 随机变量的分布函数
引例

定义
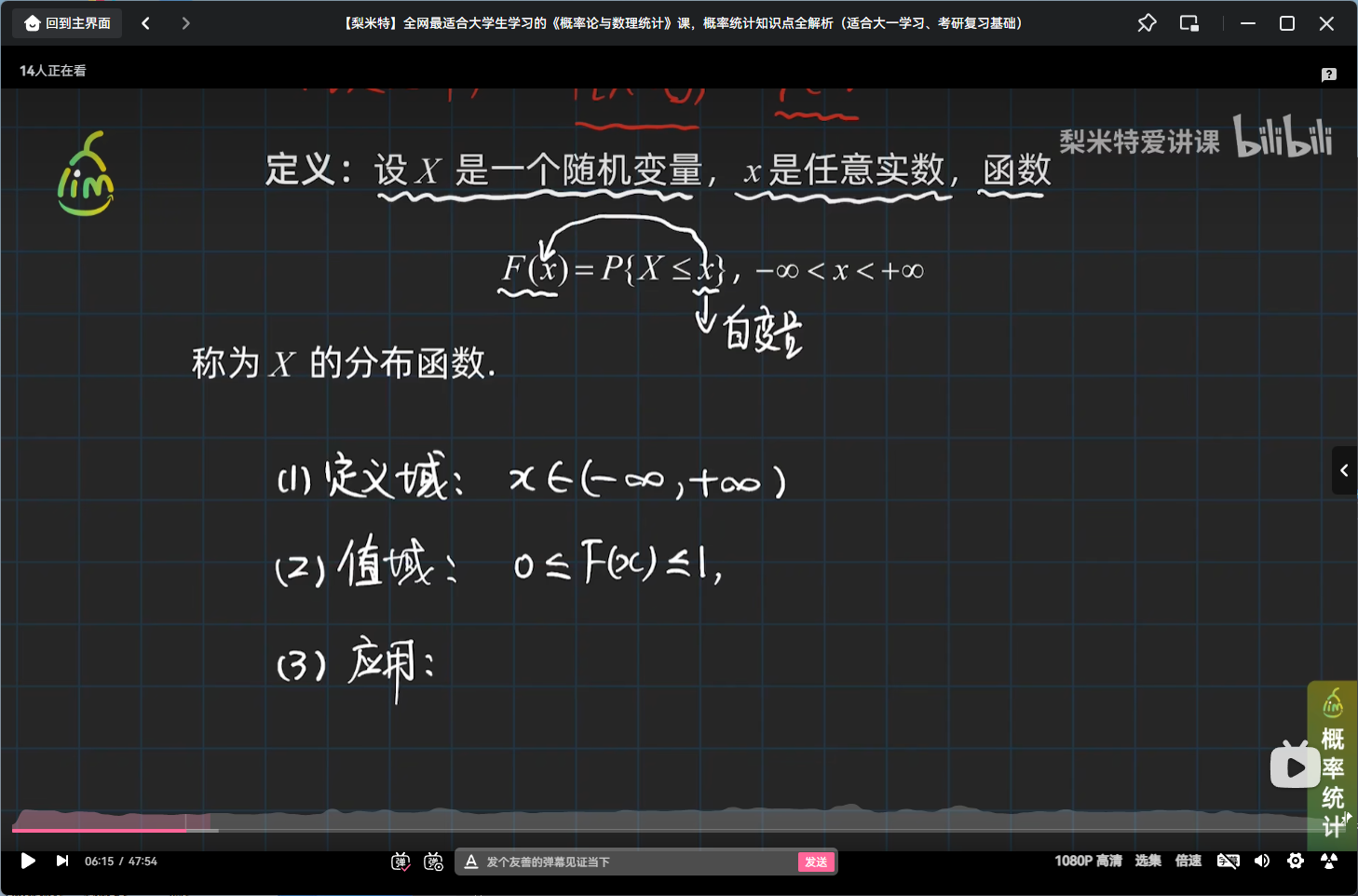
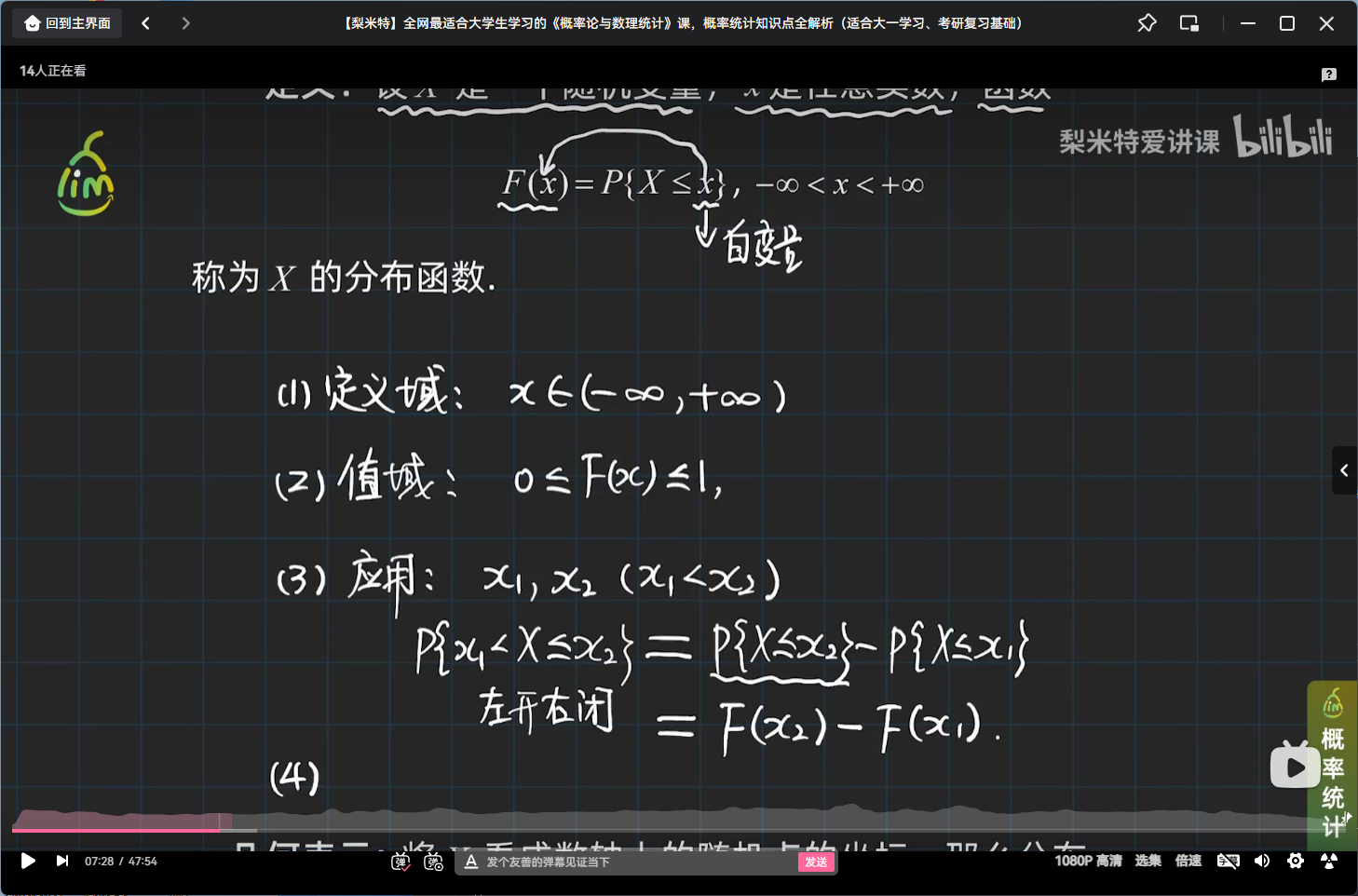

提示
从这个定义可以看出:
- 分布函数是定义在(-∞,+∞)上,取值在[0,1]上的一个函数;
- 任一随机变量X都有且仅有一个分布函数,有了分布函数,就可计算与随机变量X相关事件的概率问题。
性质

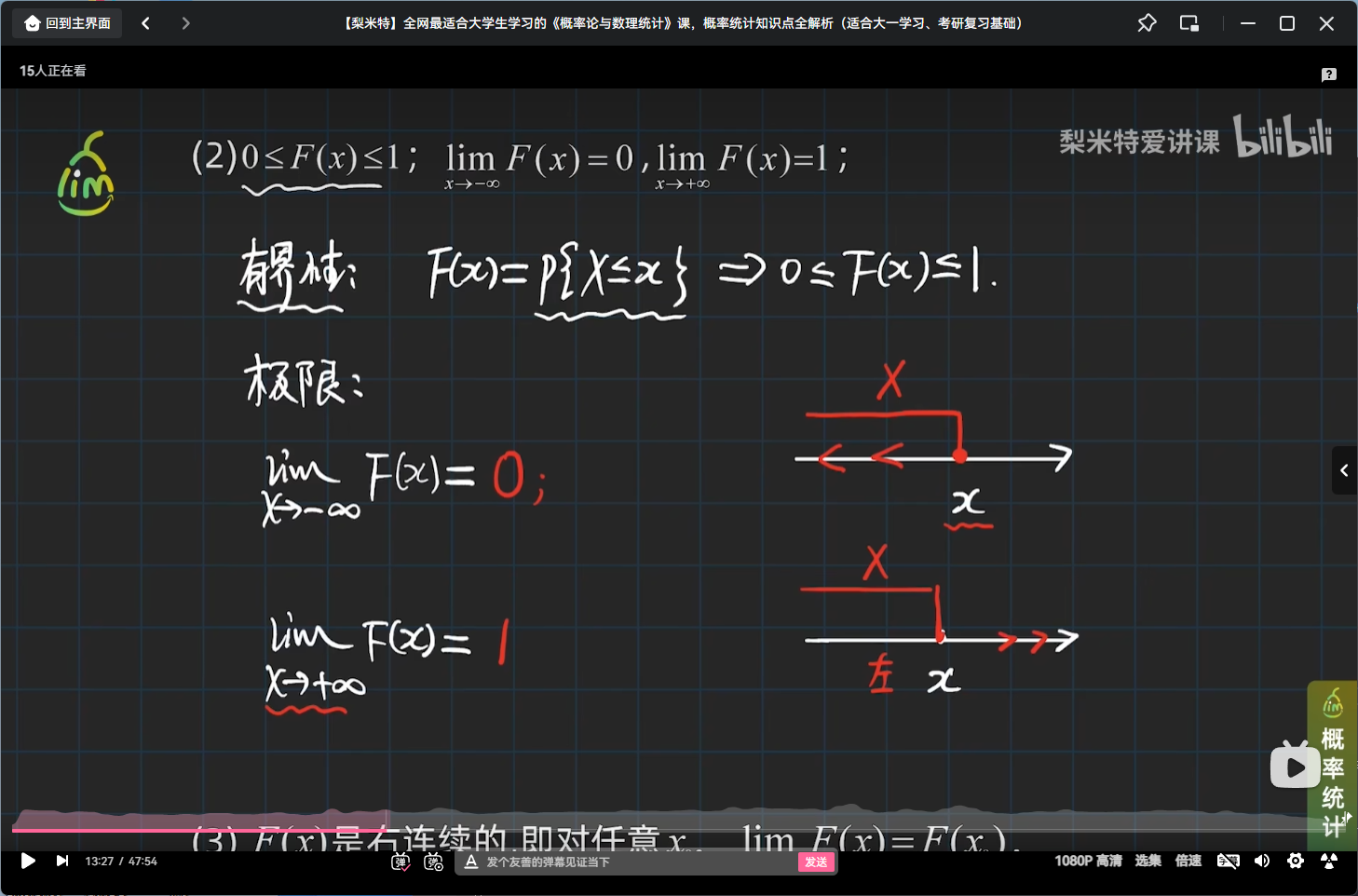

举个随机变量的分布函数的栗子
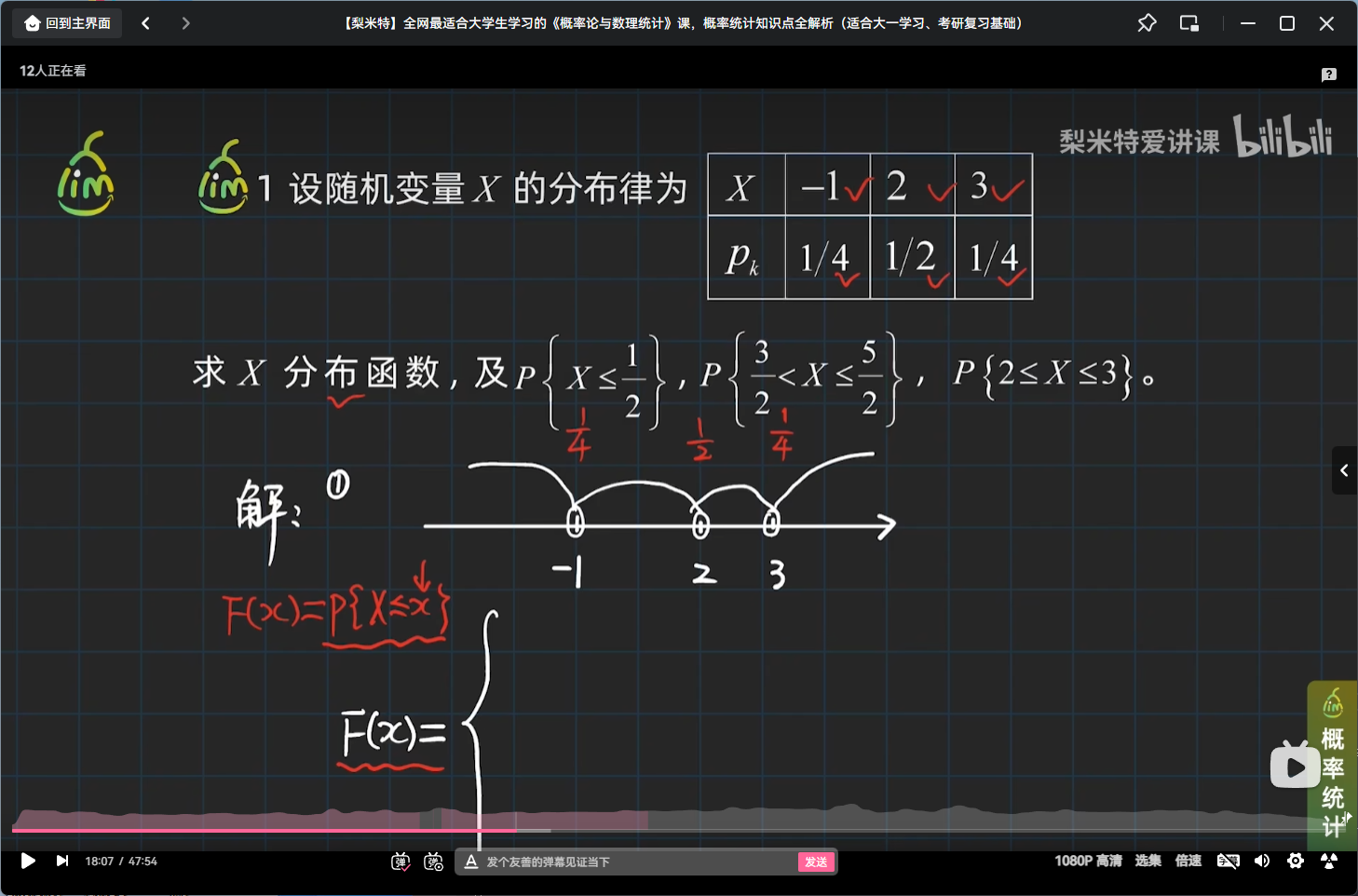

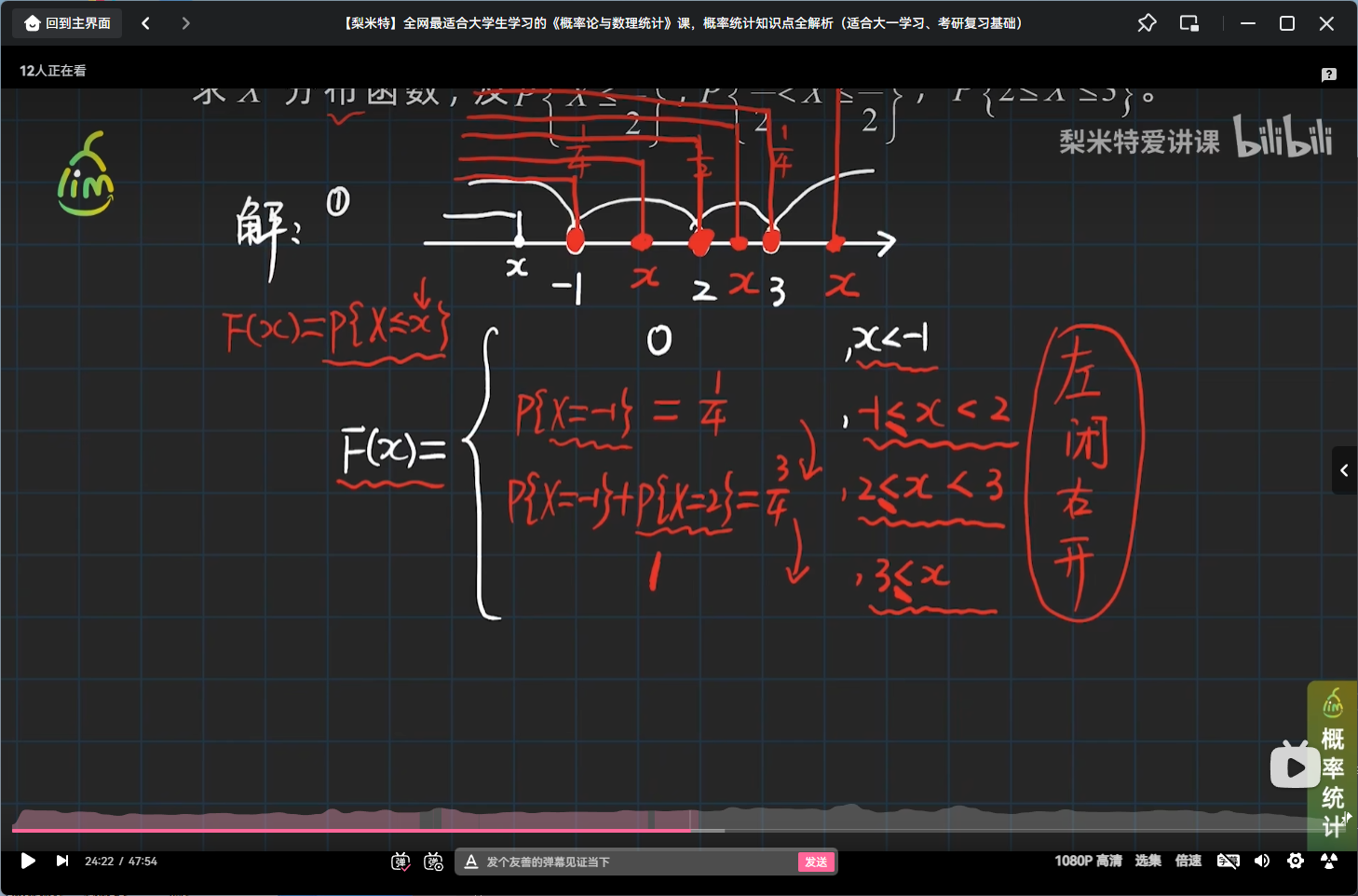
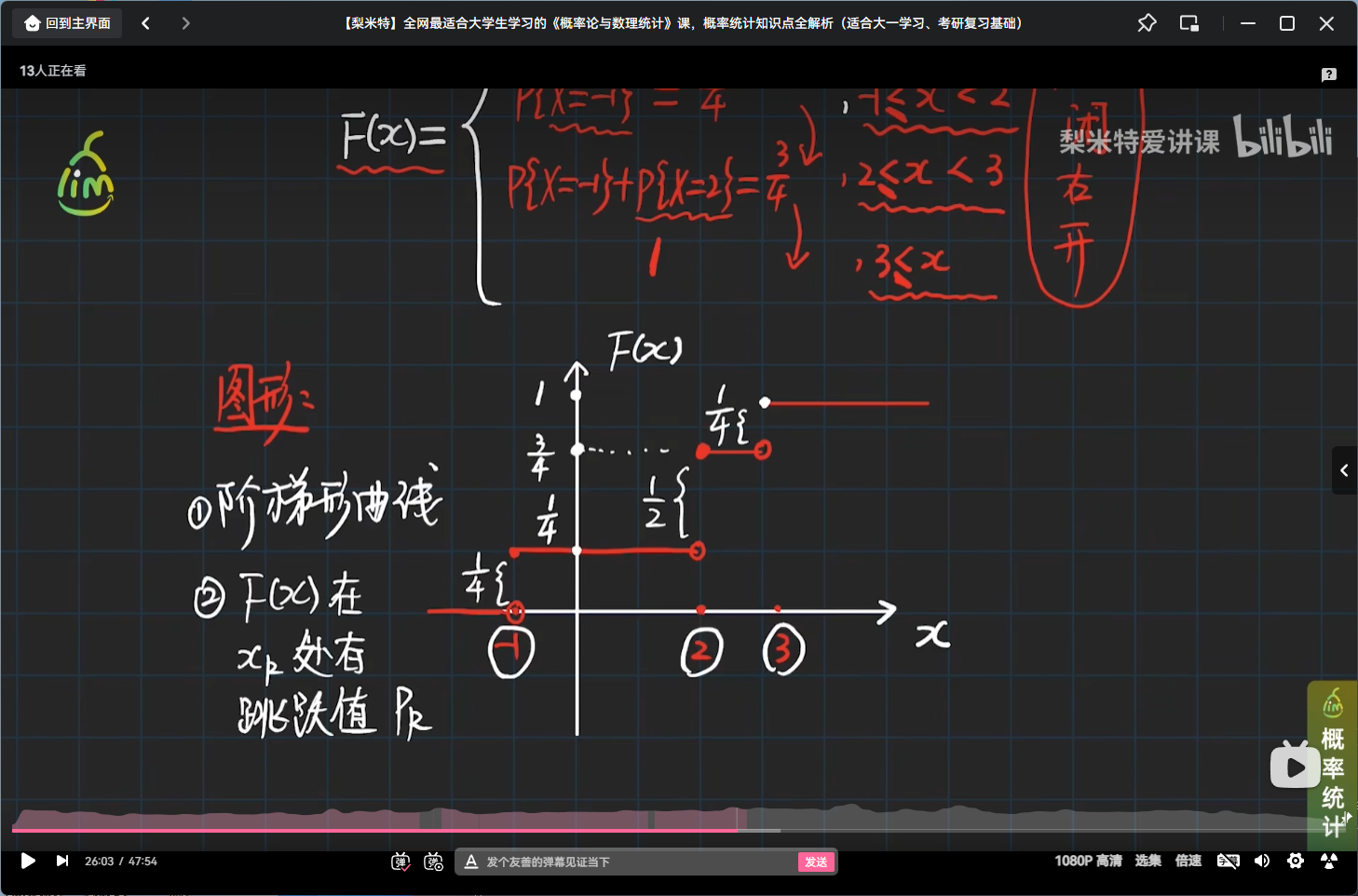
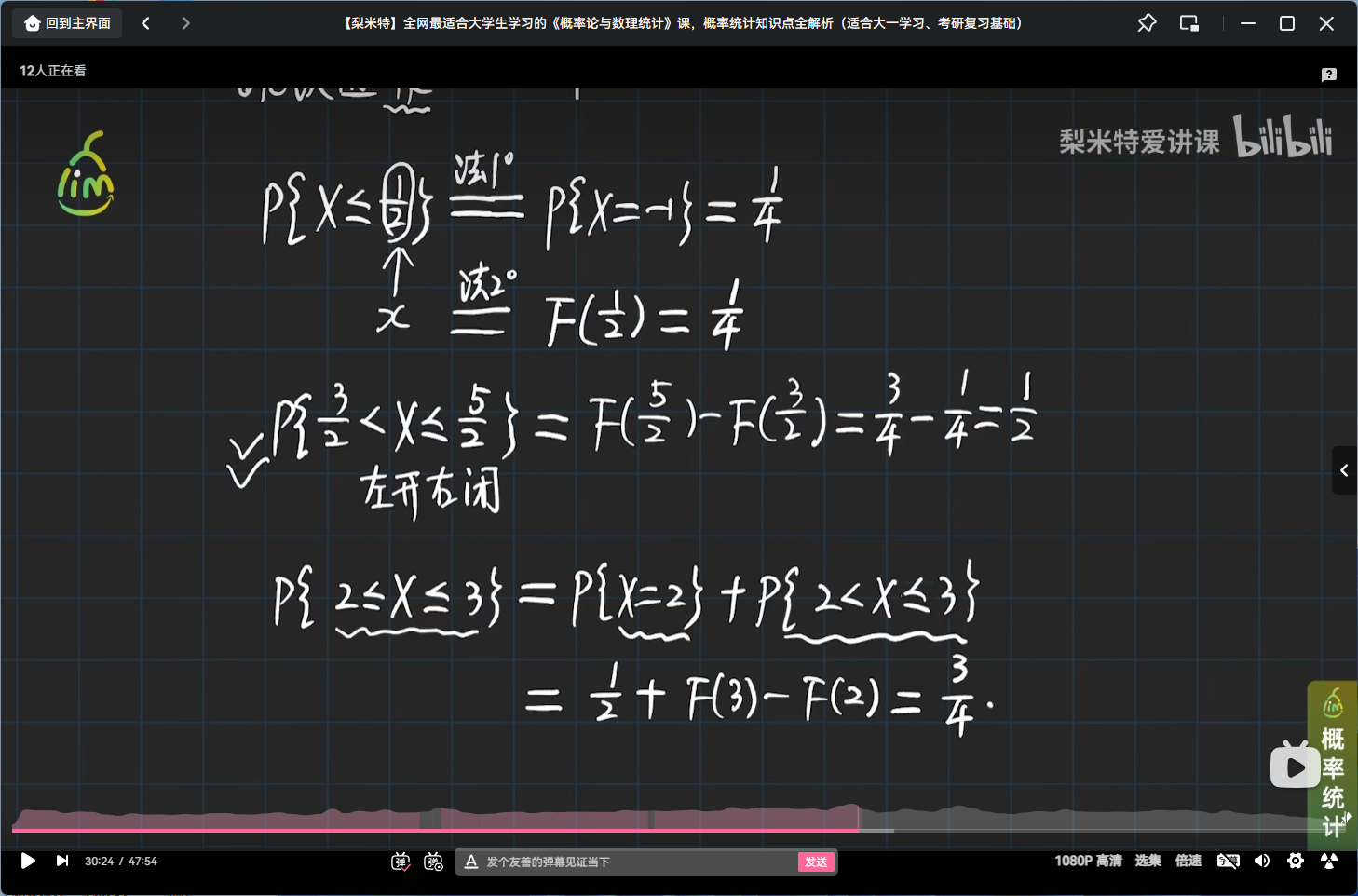
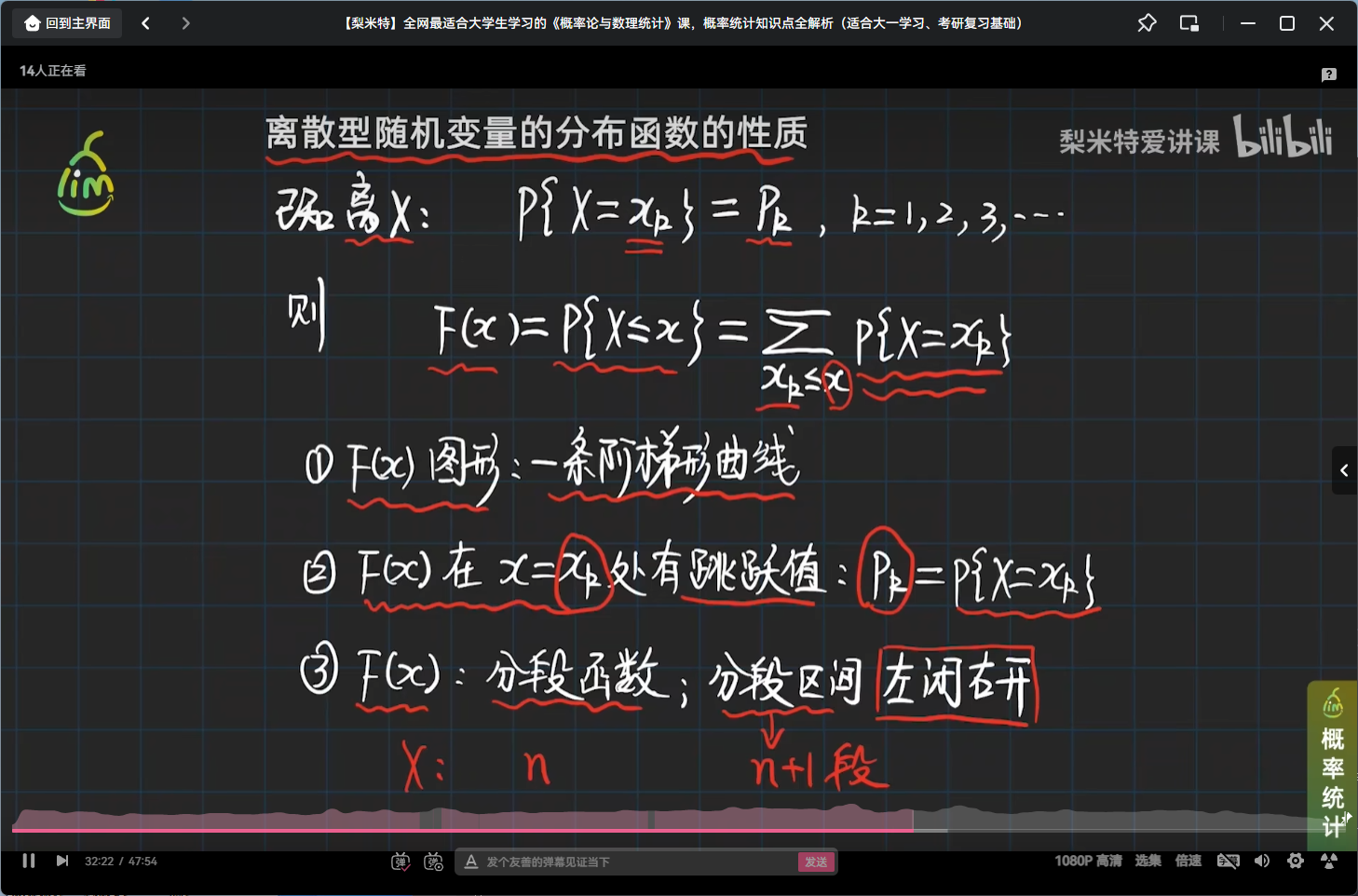
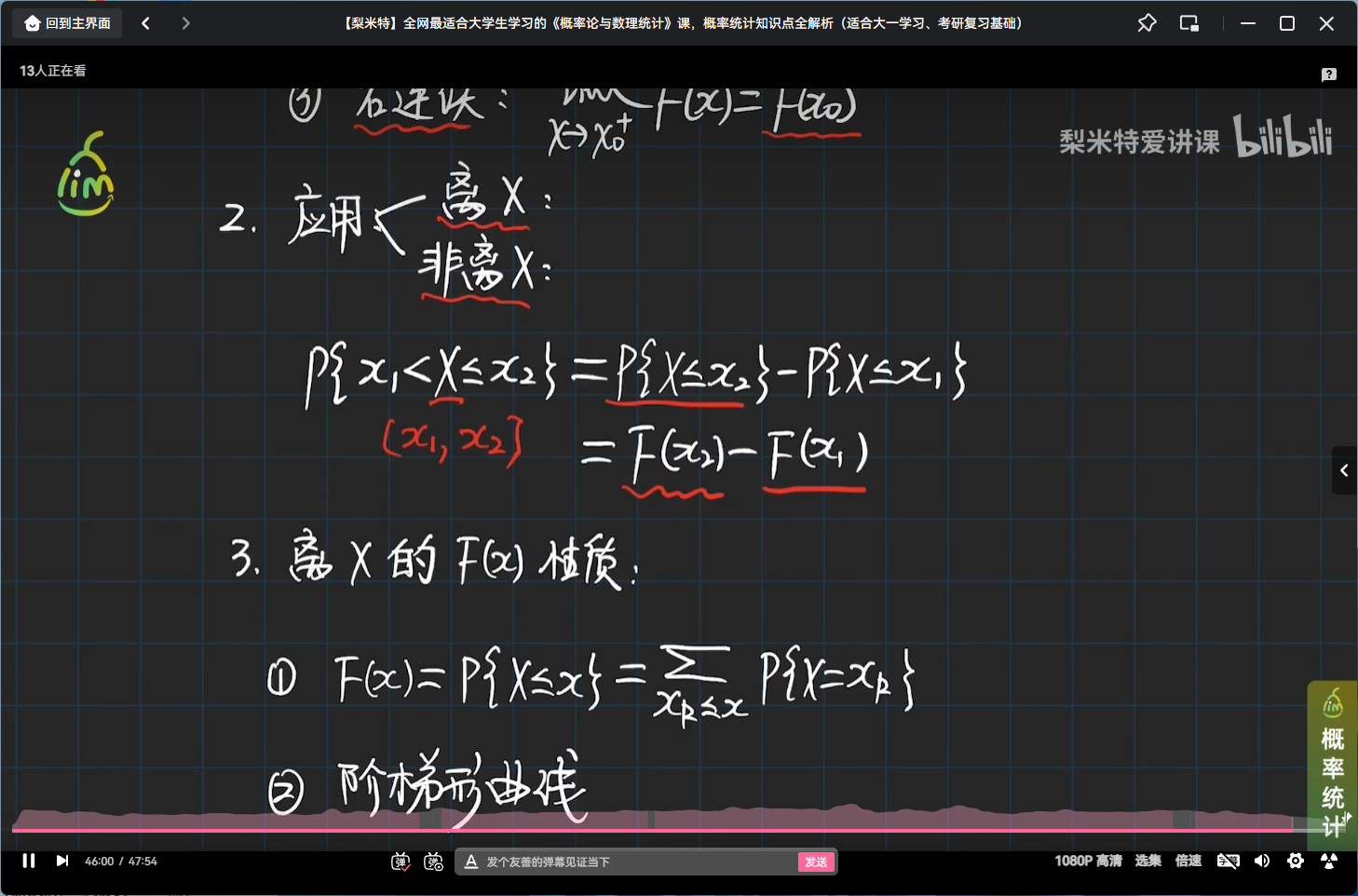
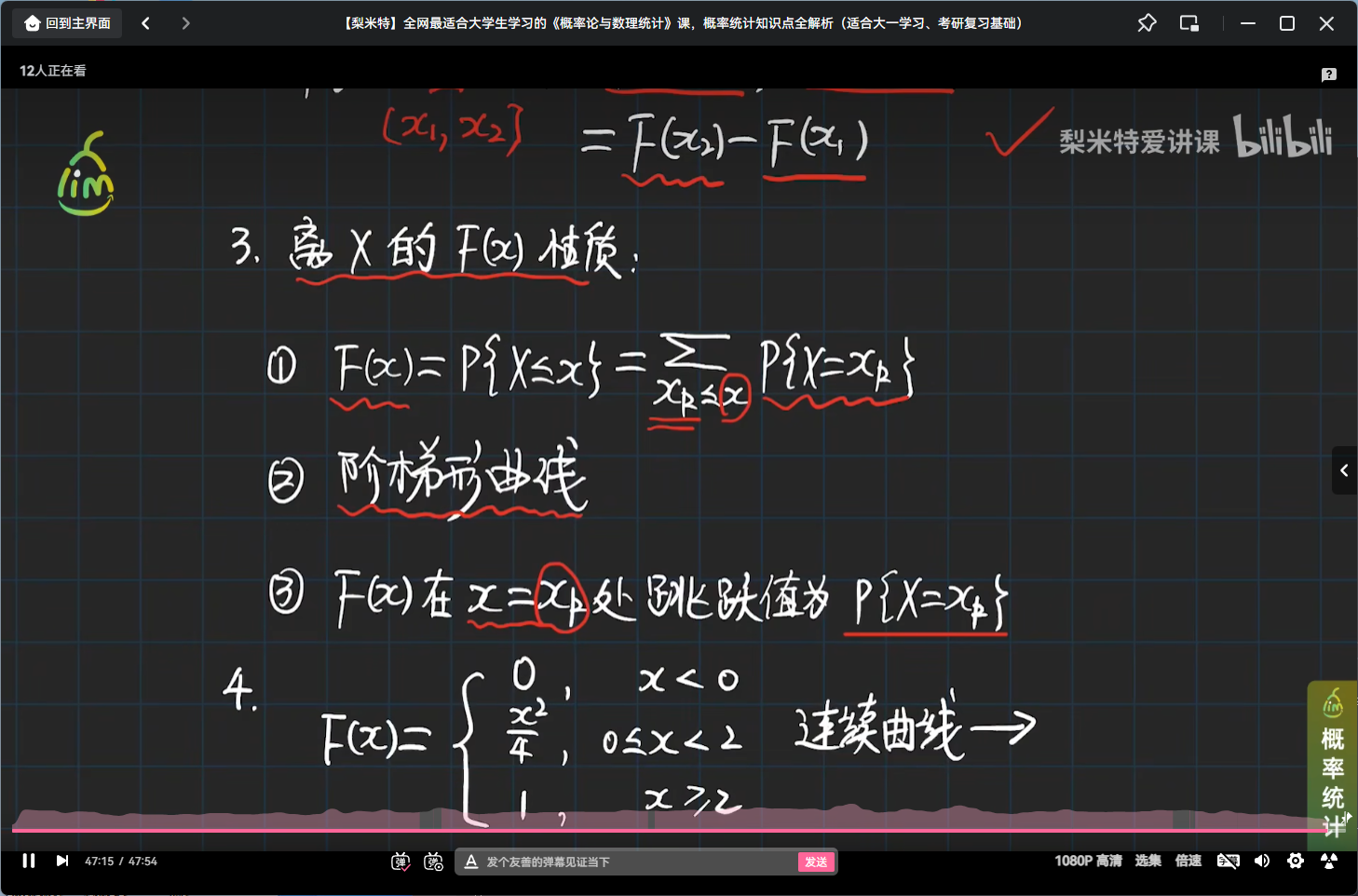
离散型随机变量分布函数的性质
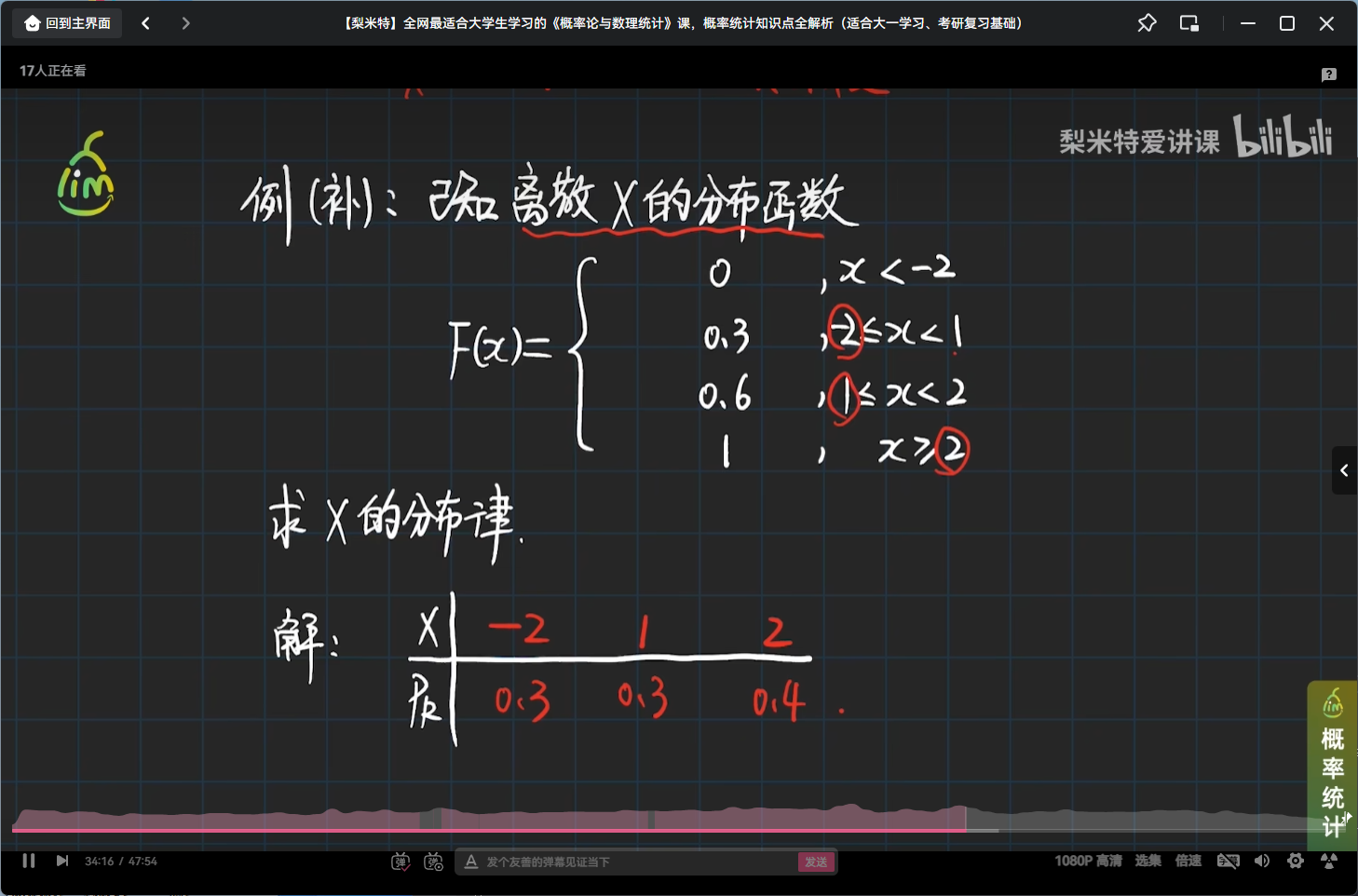
举个离散型随机变量分布函数的性质的栗子
非离散型随机变量分布函数引例
引例
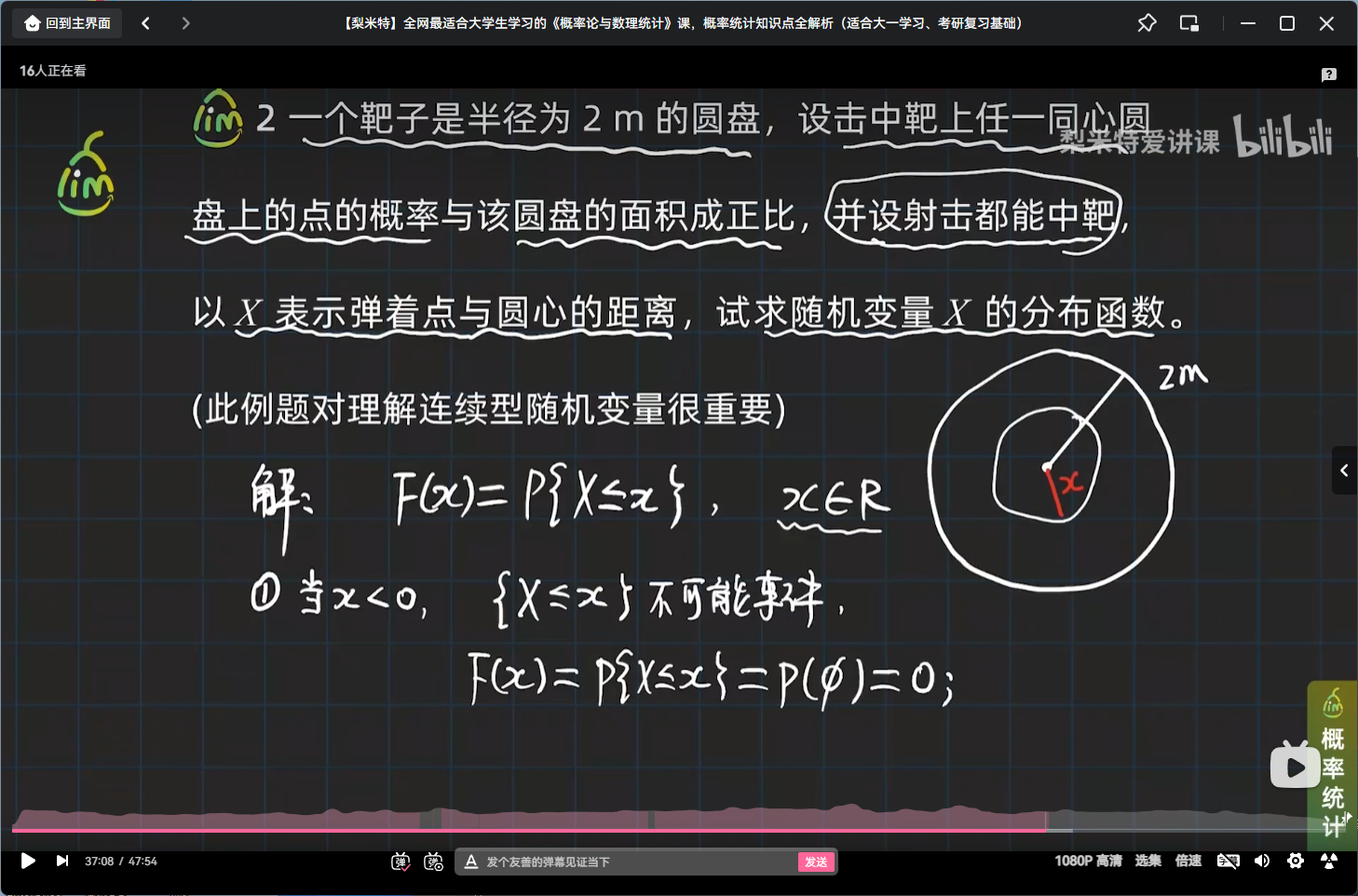

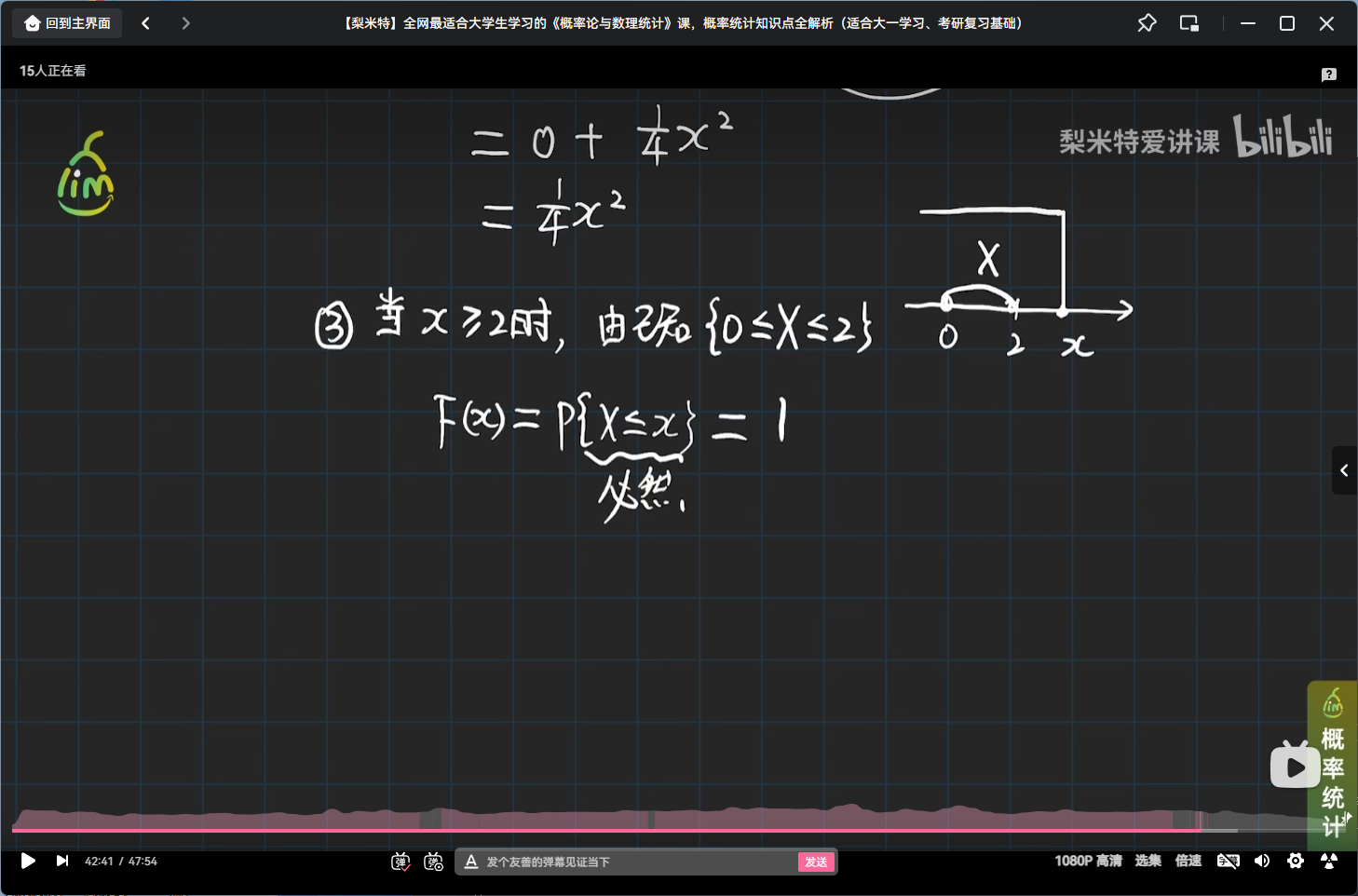
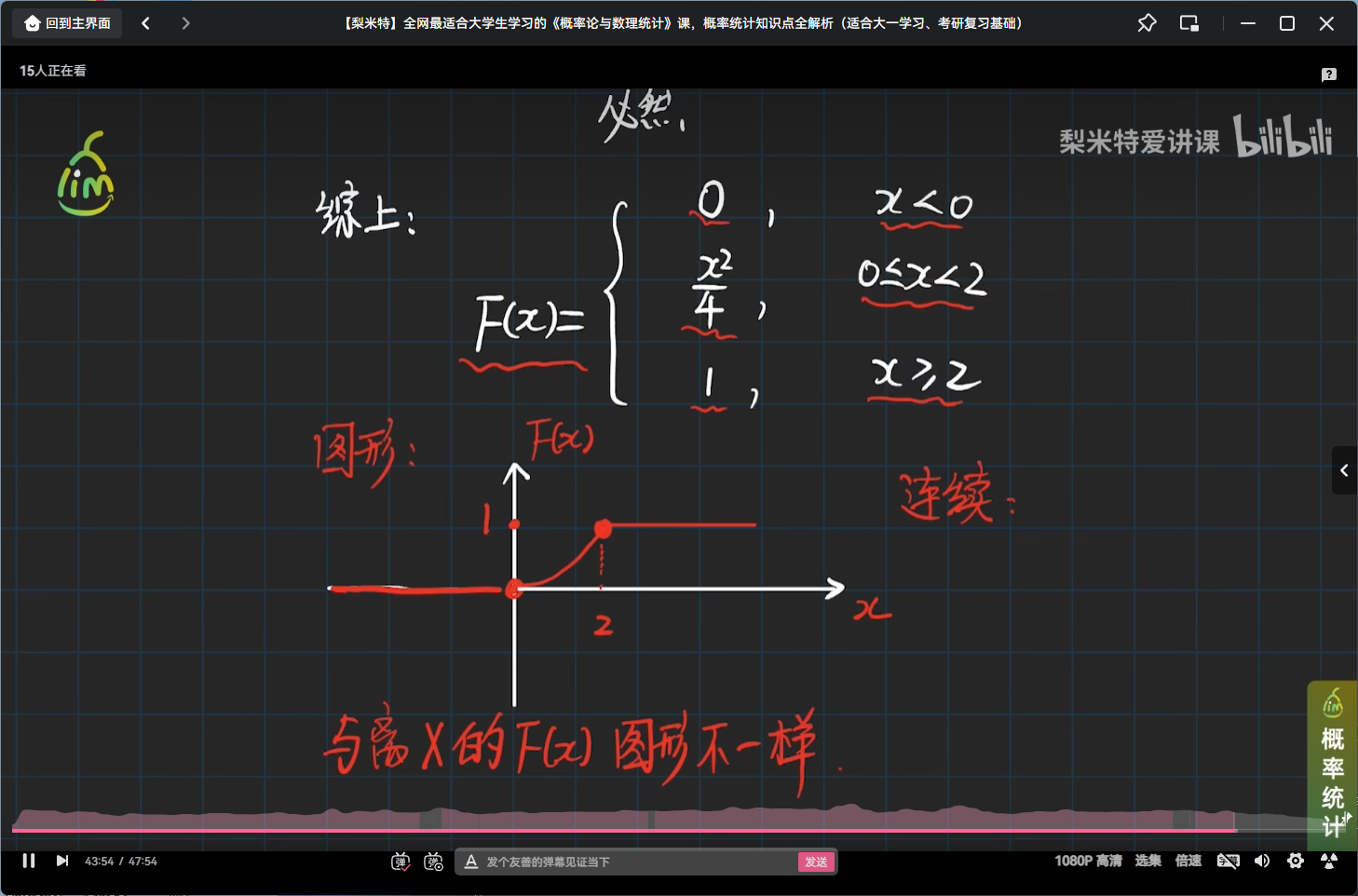
小结
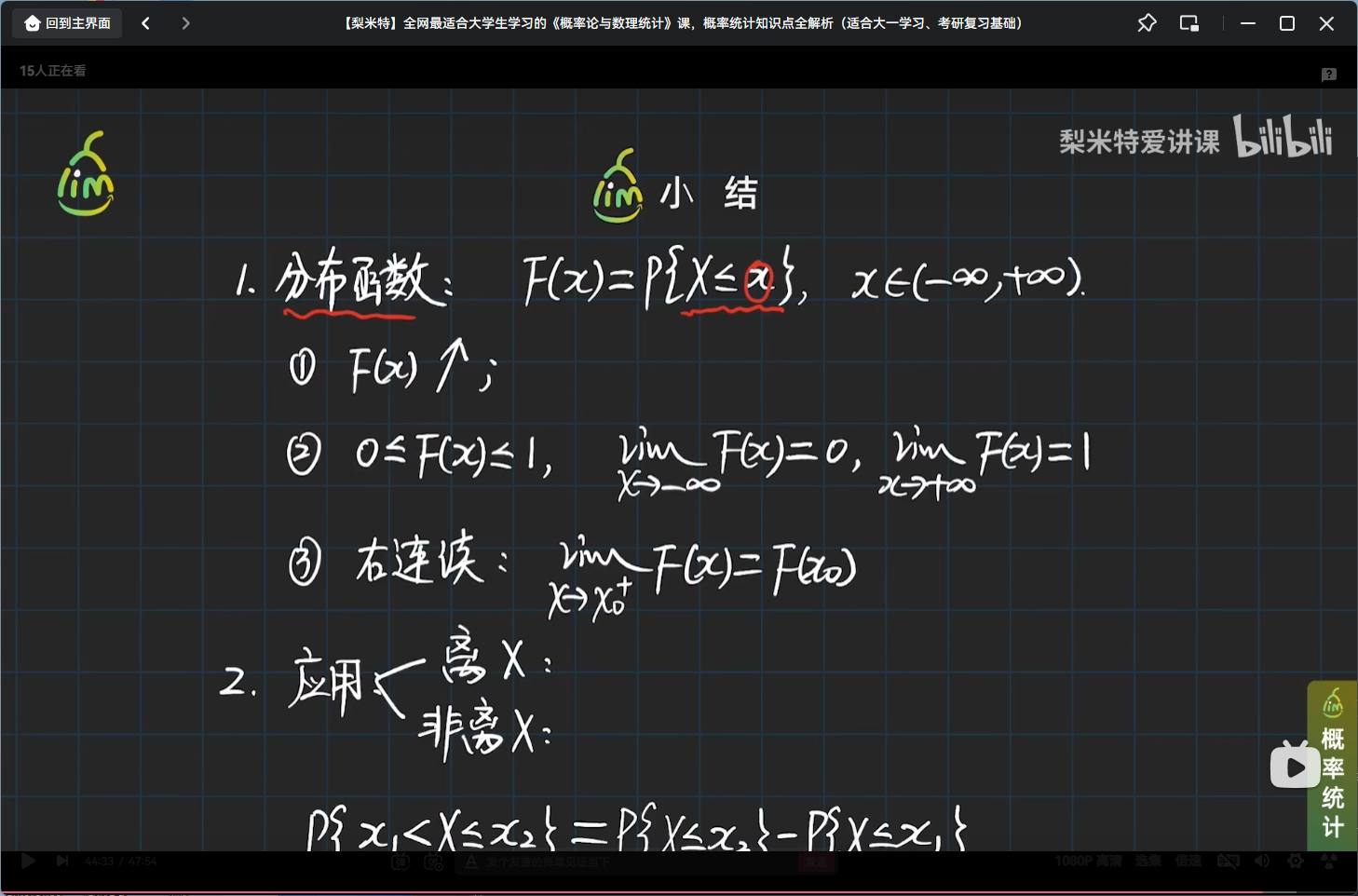
# 连续型随机变量及其密度函数
连续型随机变量的取值充满了数轴上的一个区间(或某几个区间的并),在这个区间里有无穷不可列个实数,因此当我们描述连续型随机变量时,用来描述离散型随机变量的分布律就没法再使用了,而要改用概率密度函数来表示。
定义

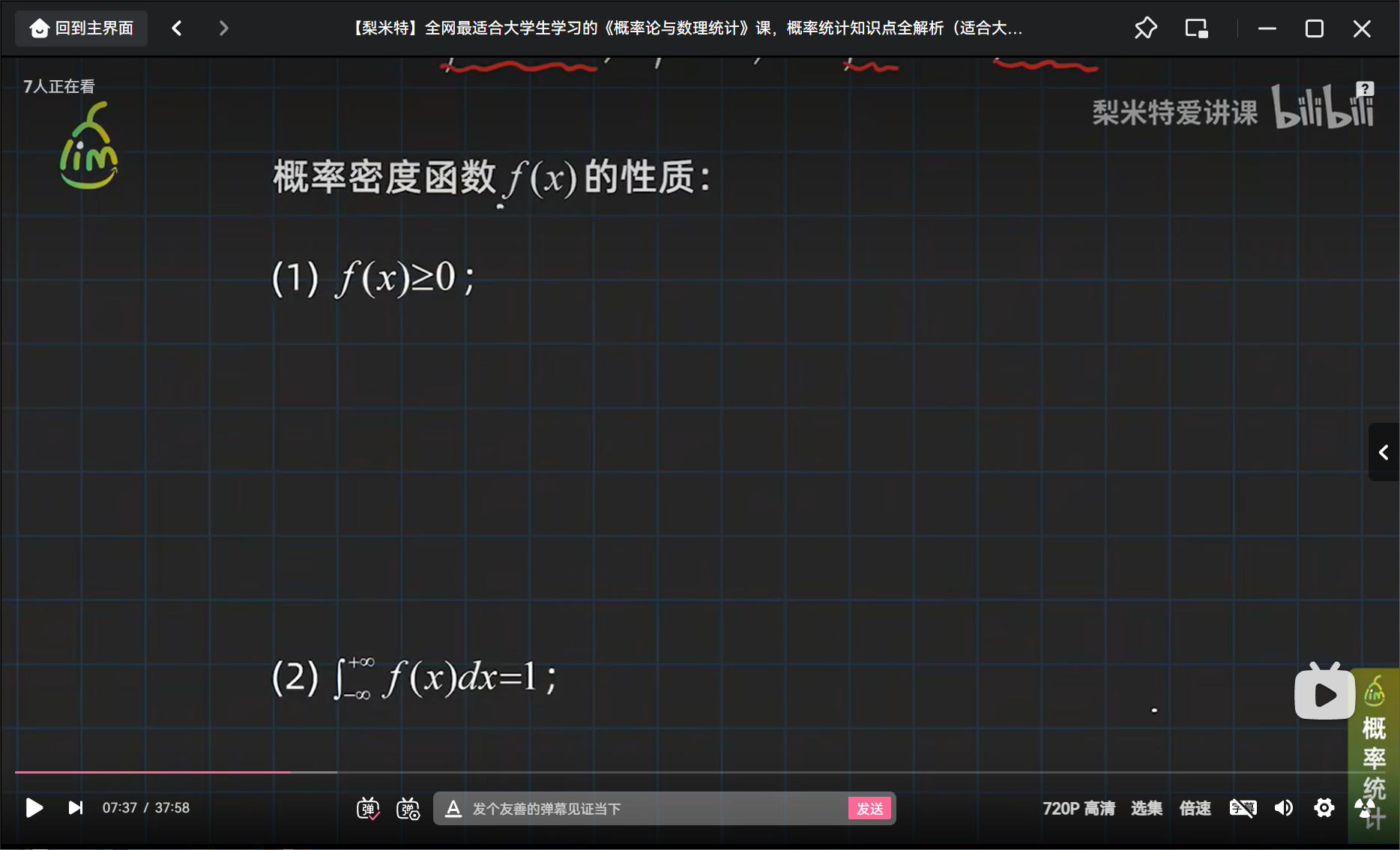
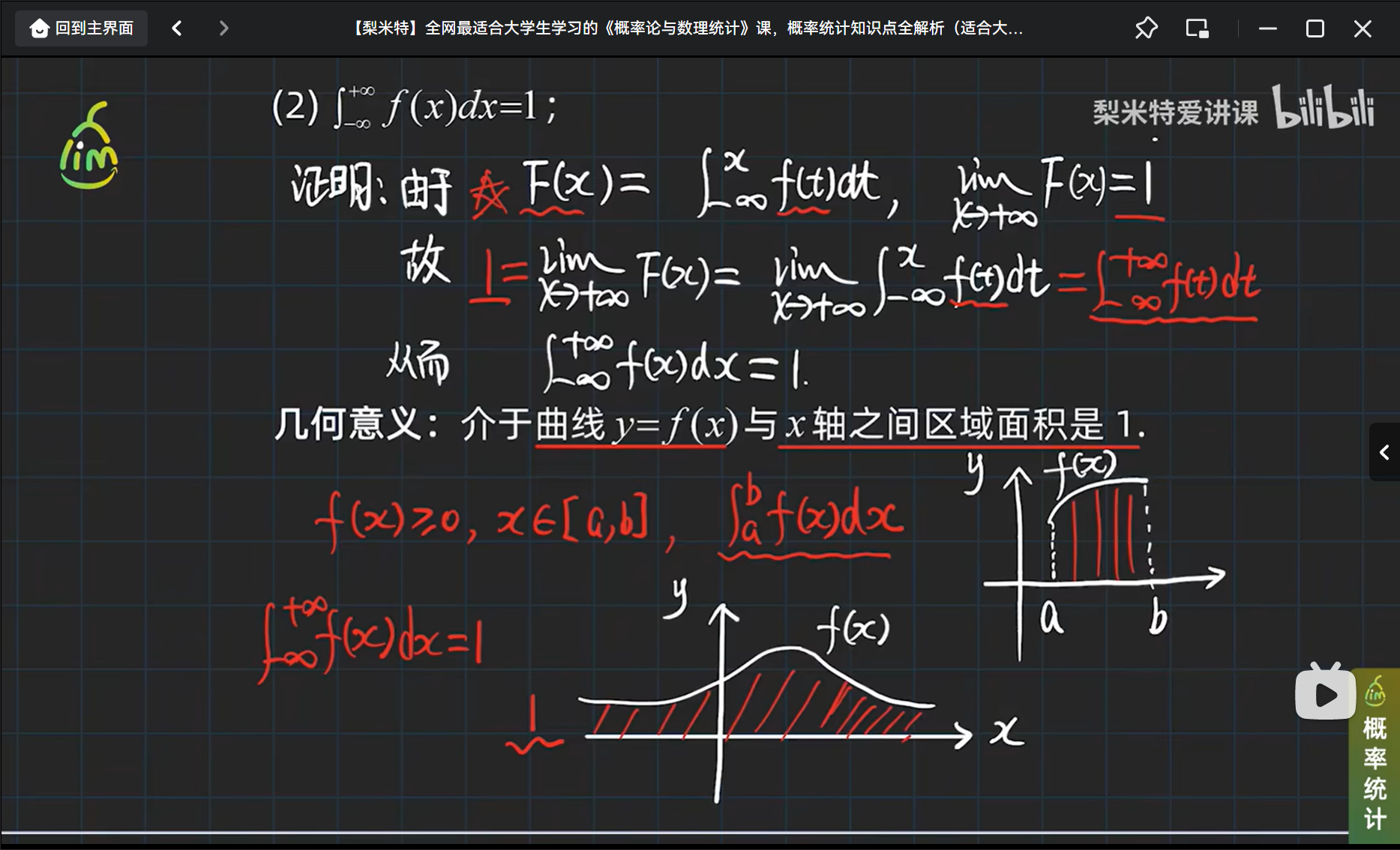
性质

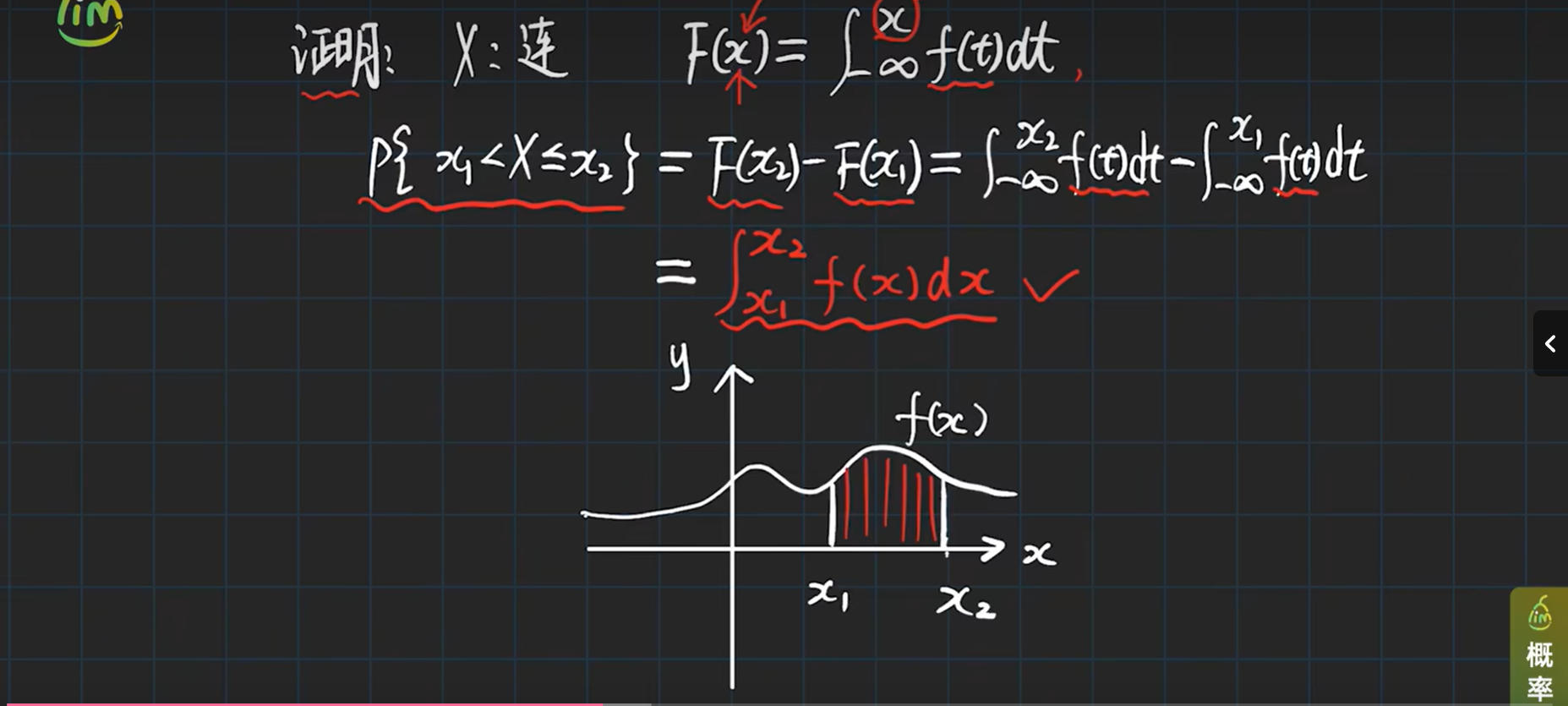
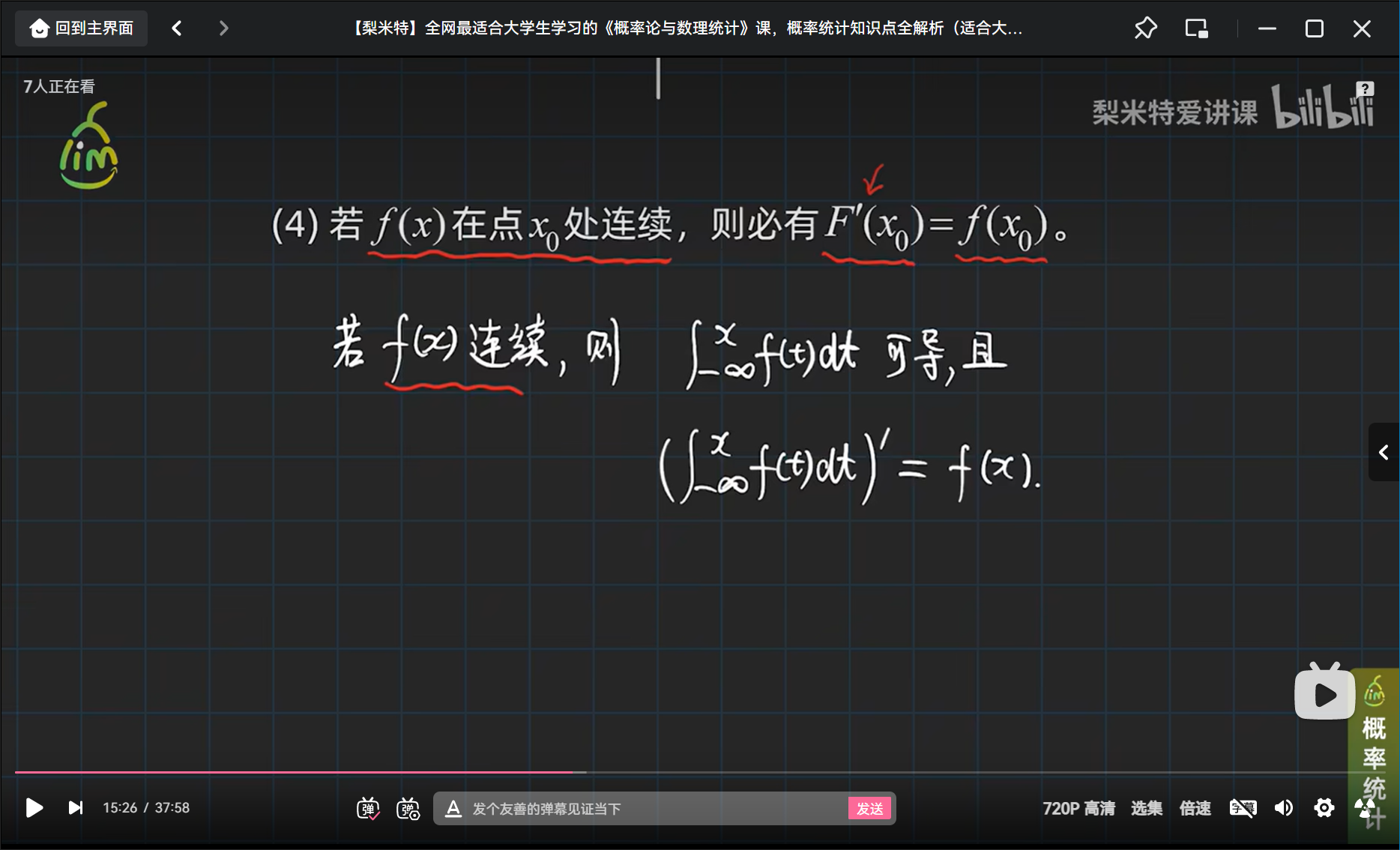
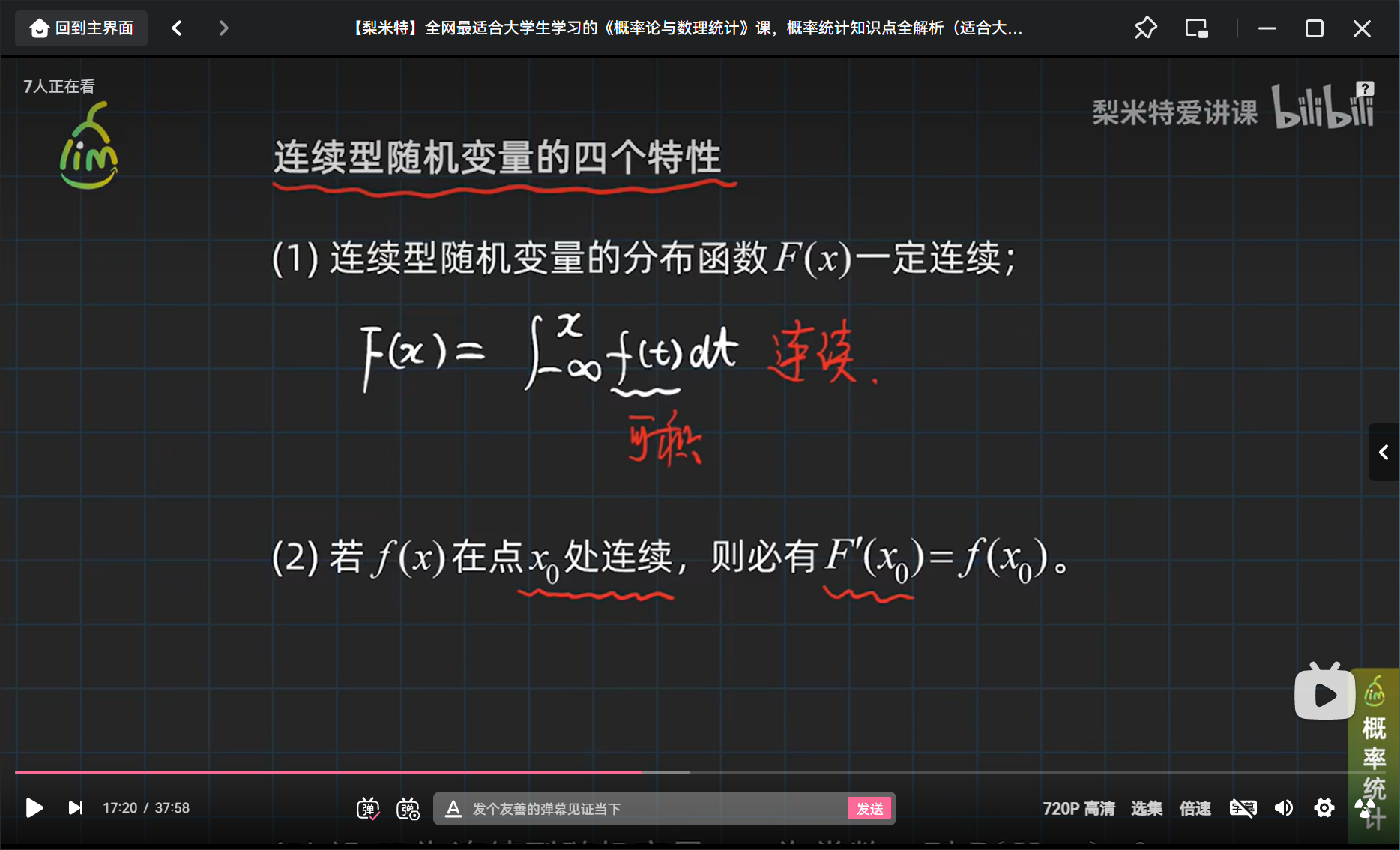
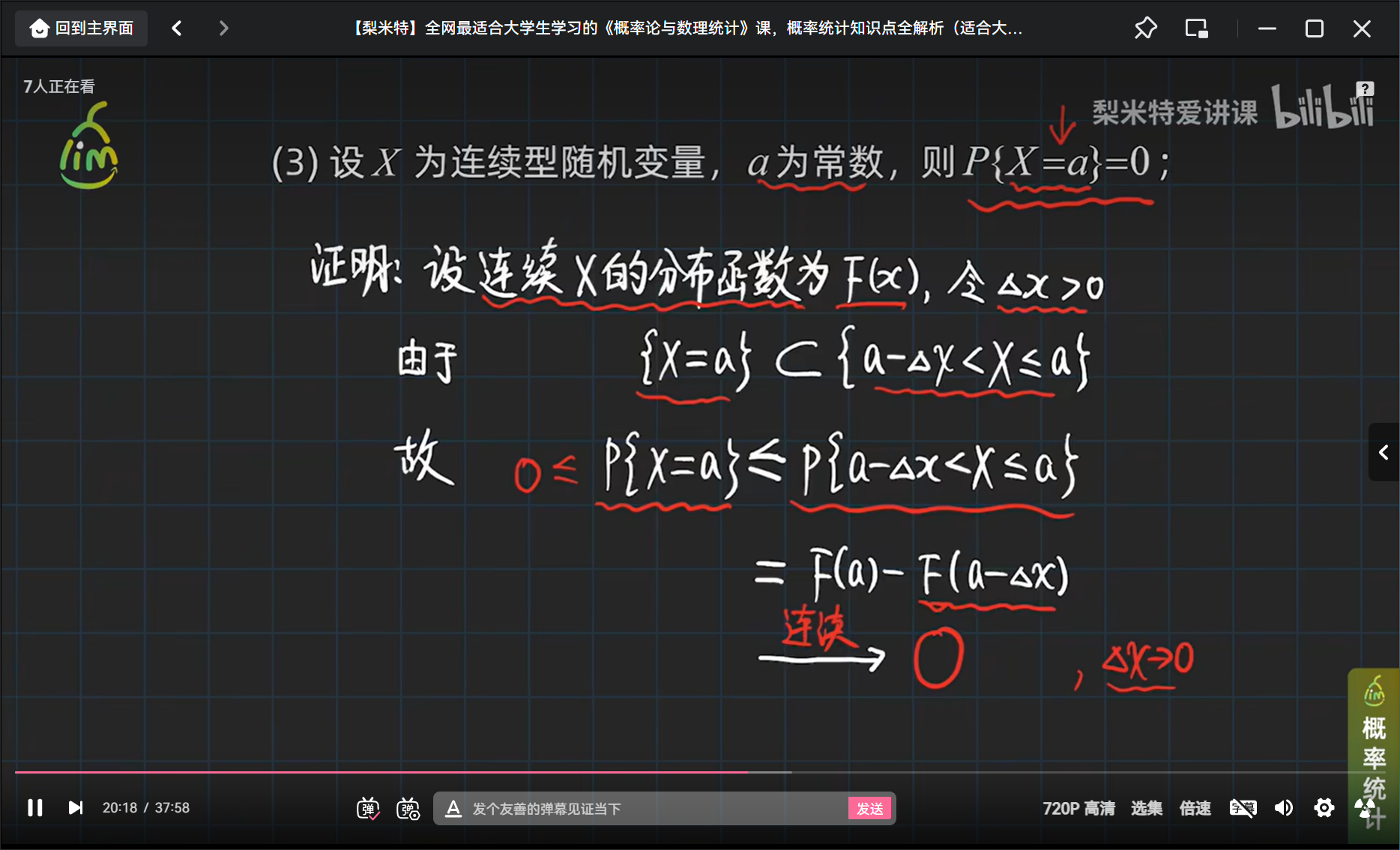
连续型随机变量的四个特征

举个连续型随机变量及其密度函数的栗子
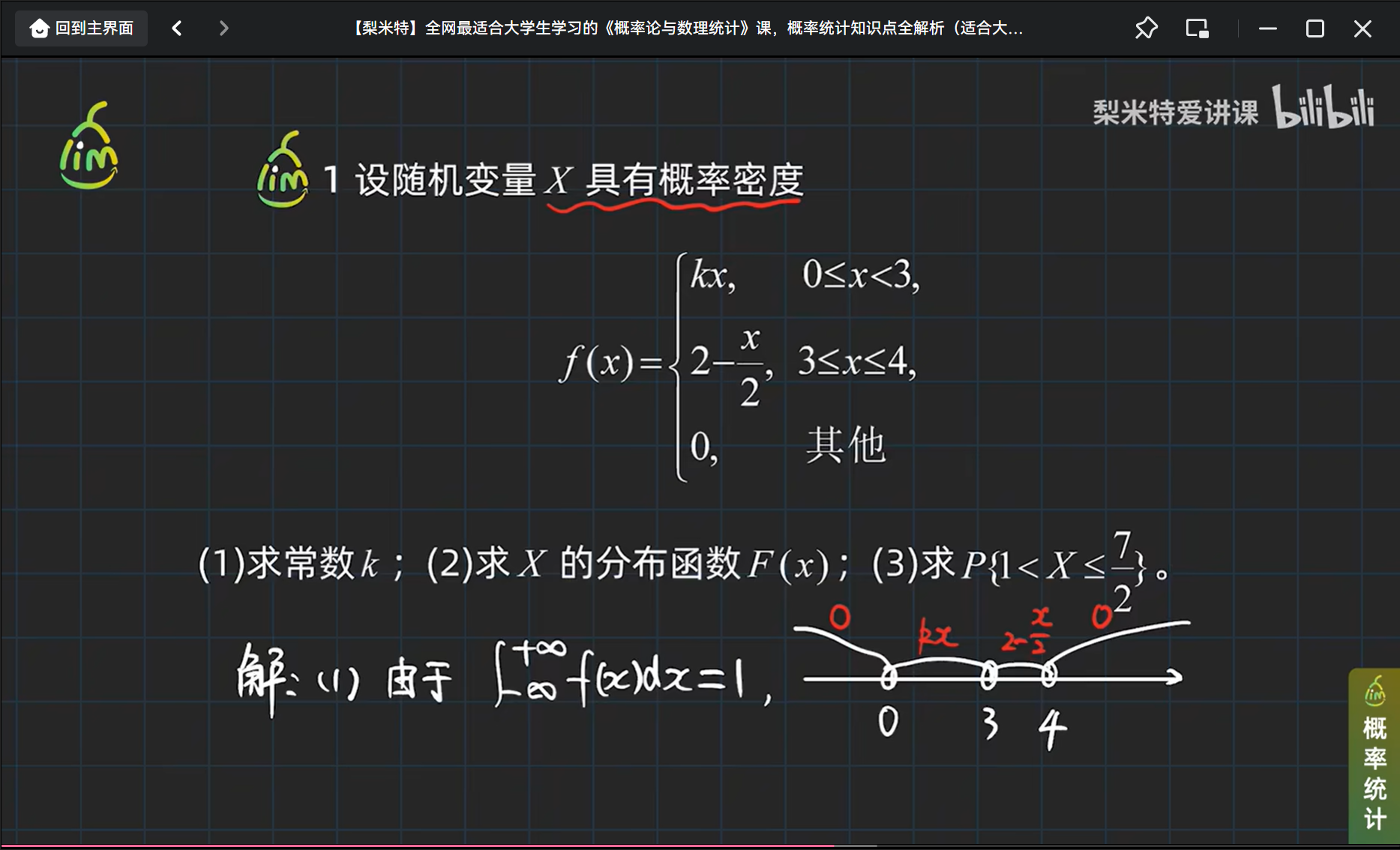
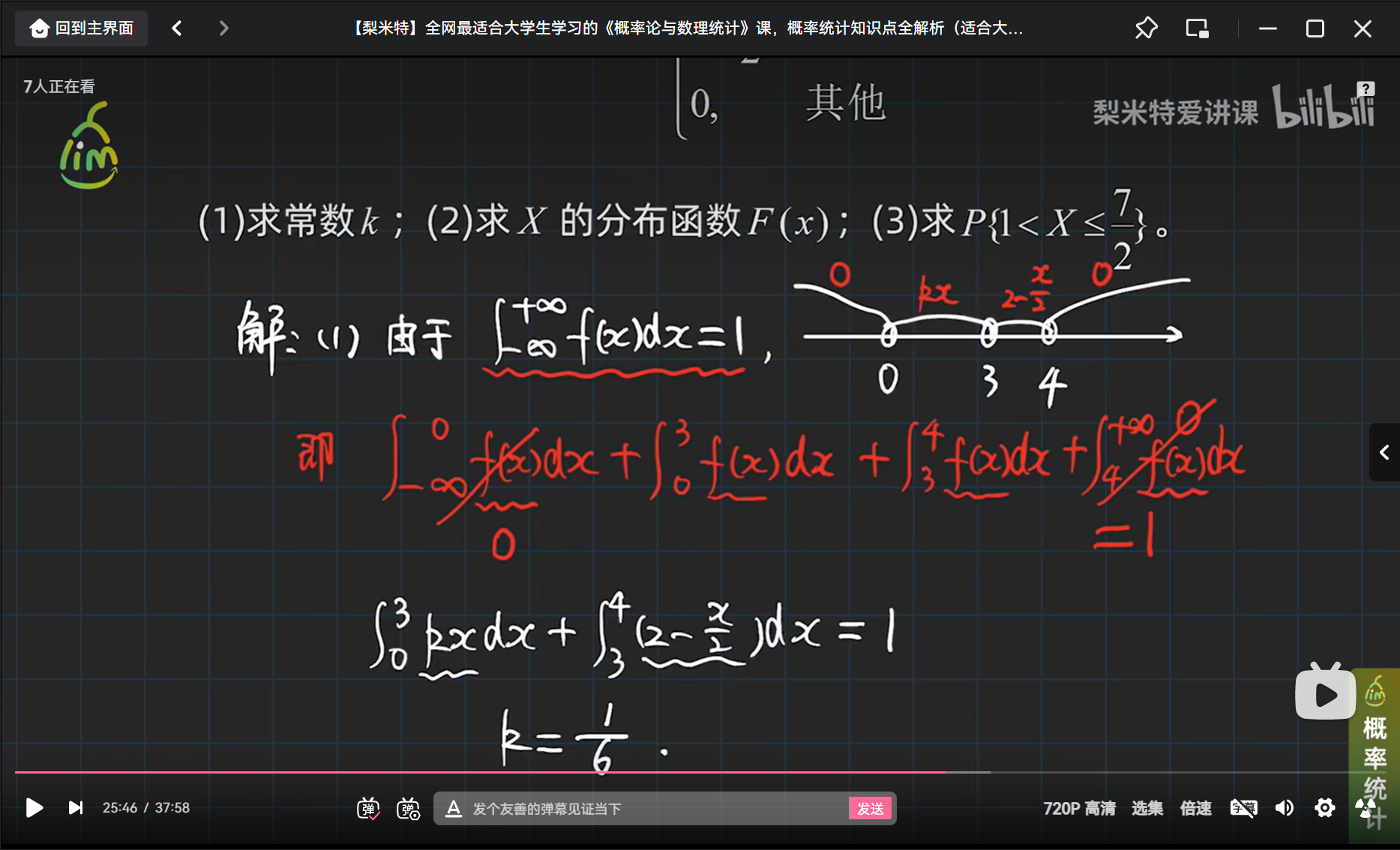
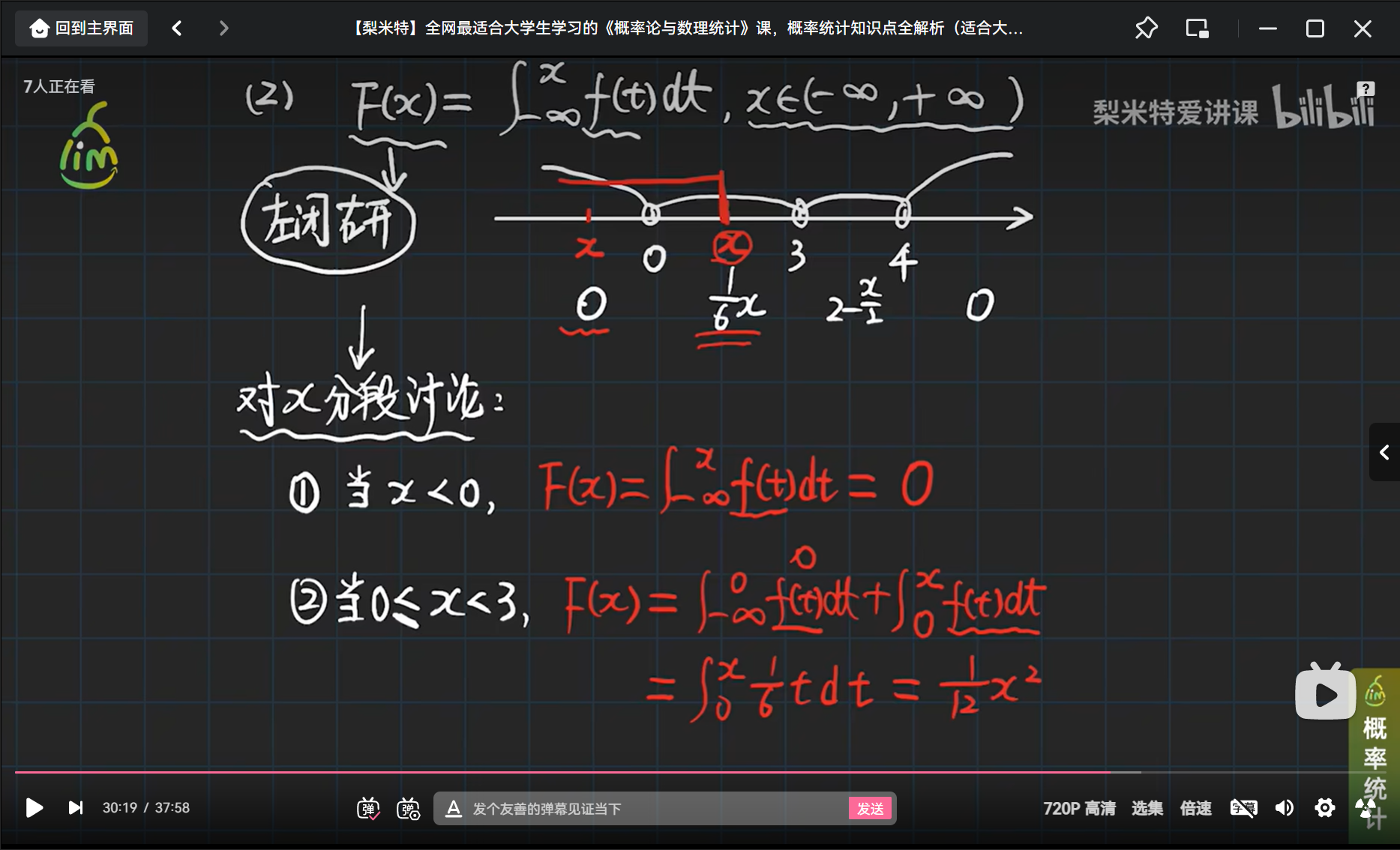
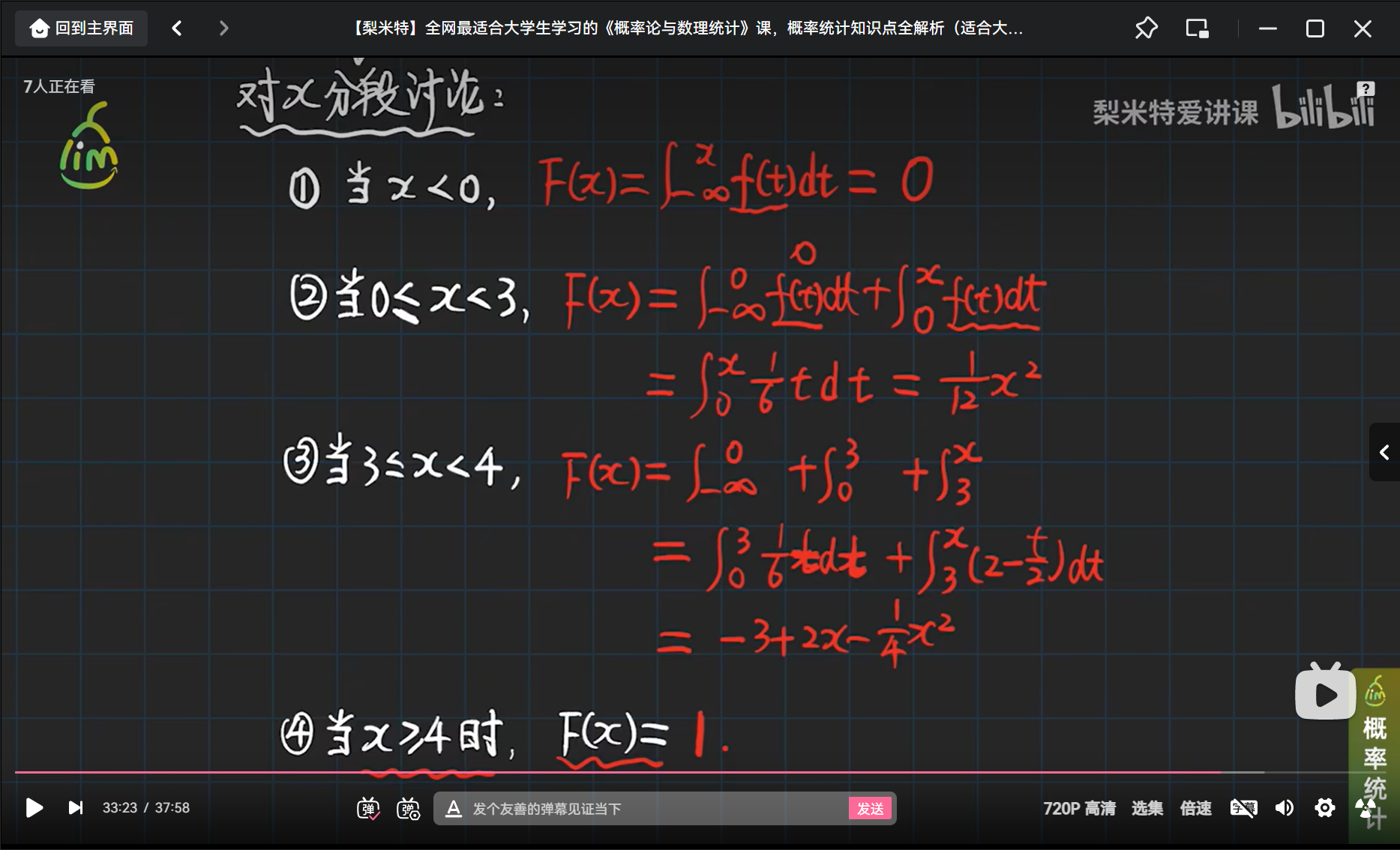
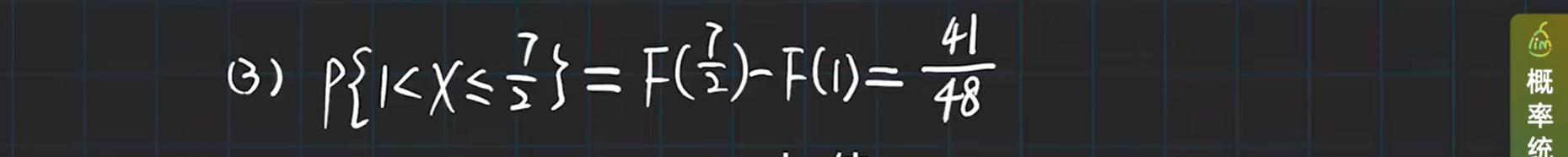
小结 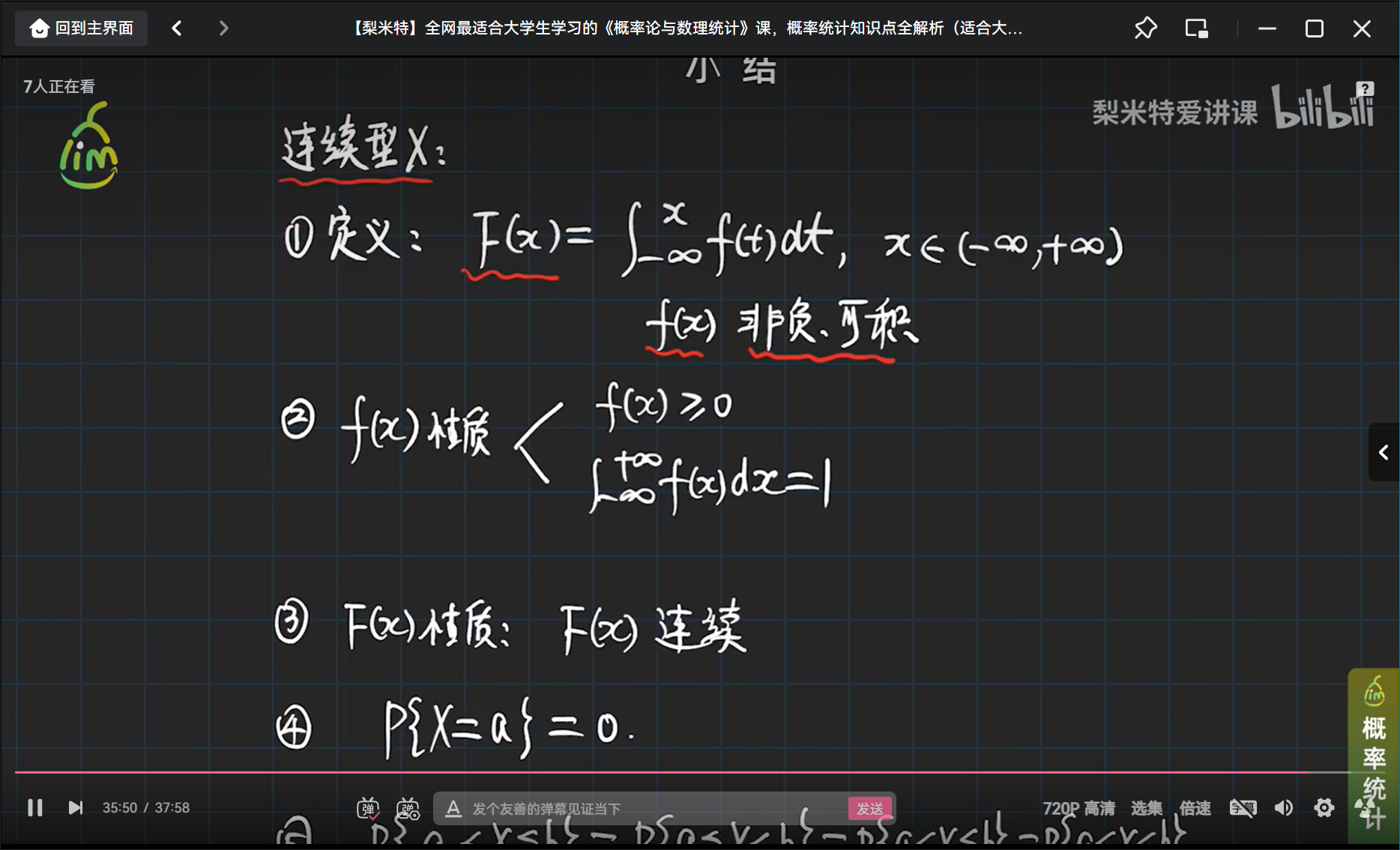
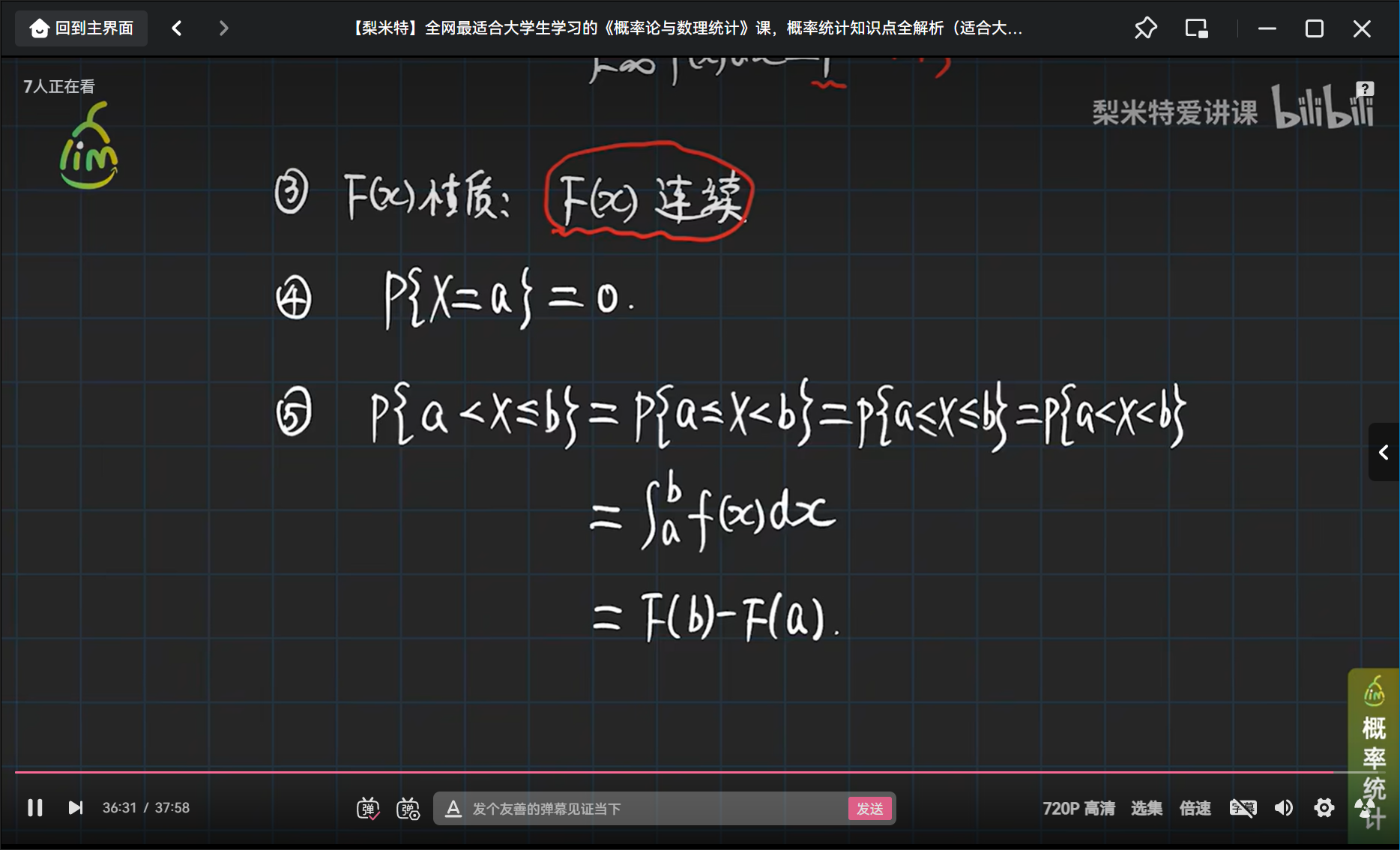
# 常用的离散型随机变量
# 最简单的离散分布:0-1分布
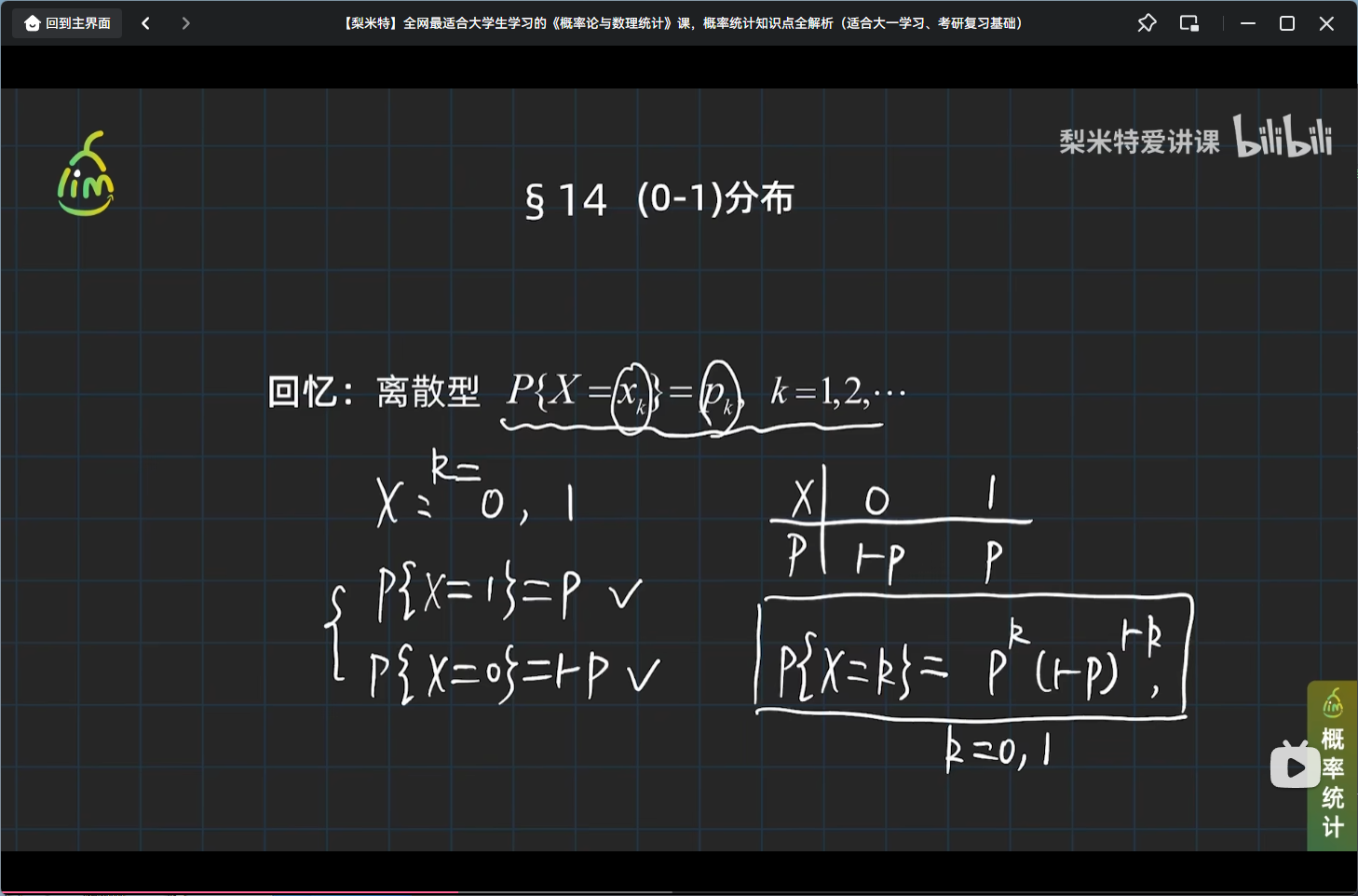
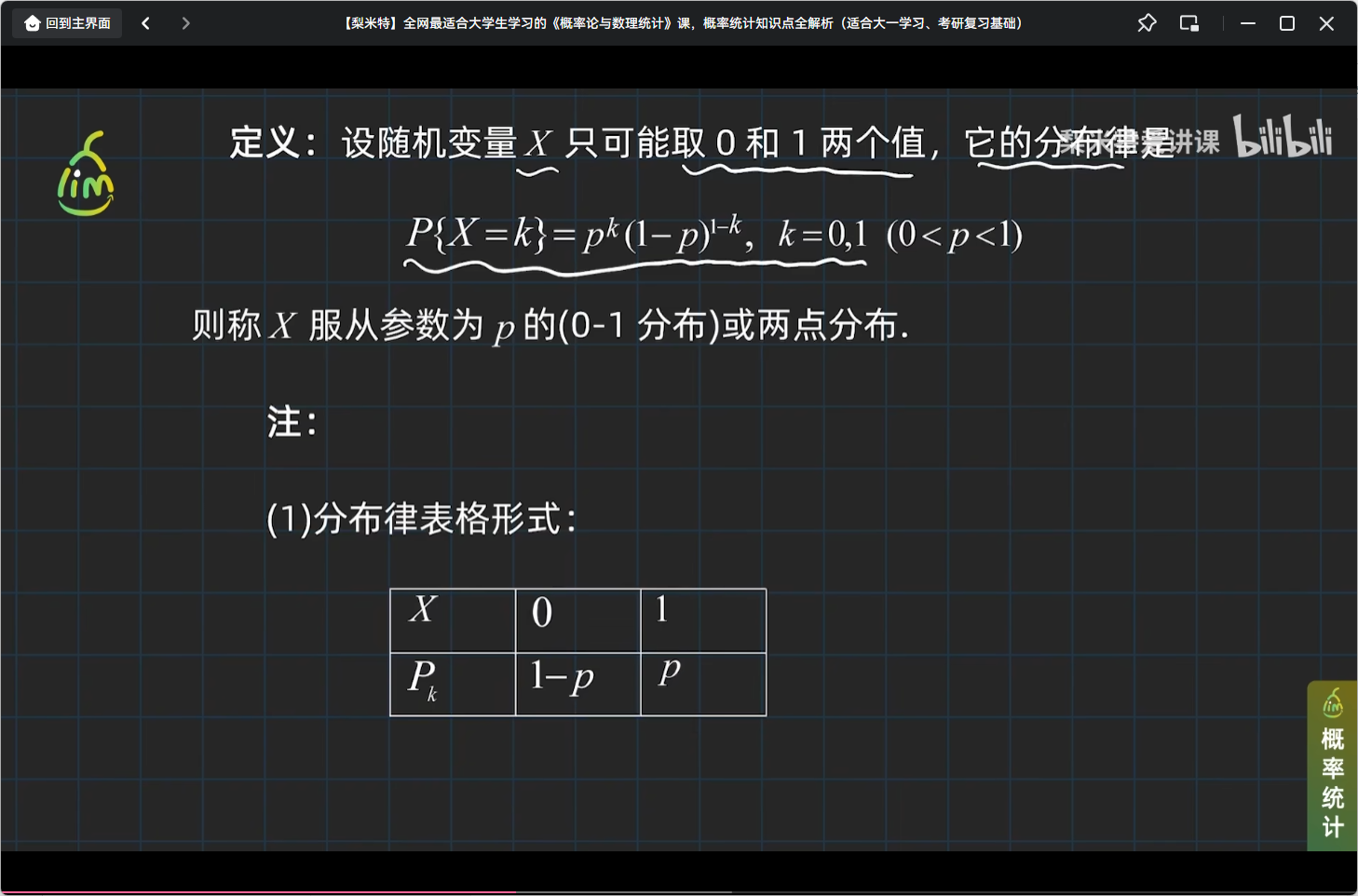
举个0-1分布的栗子
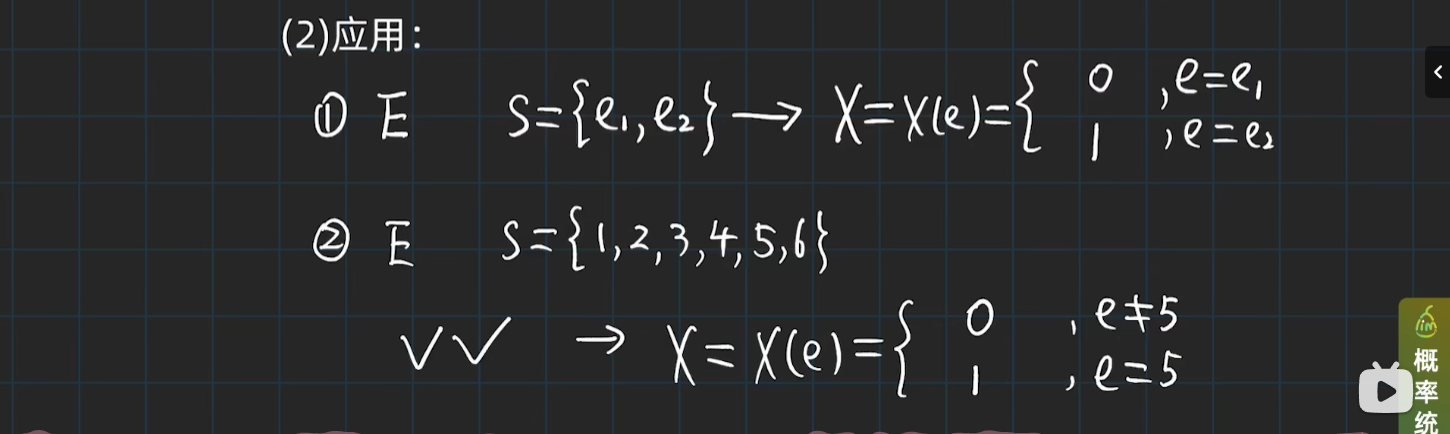
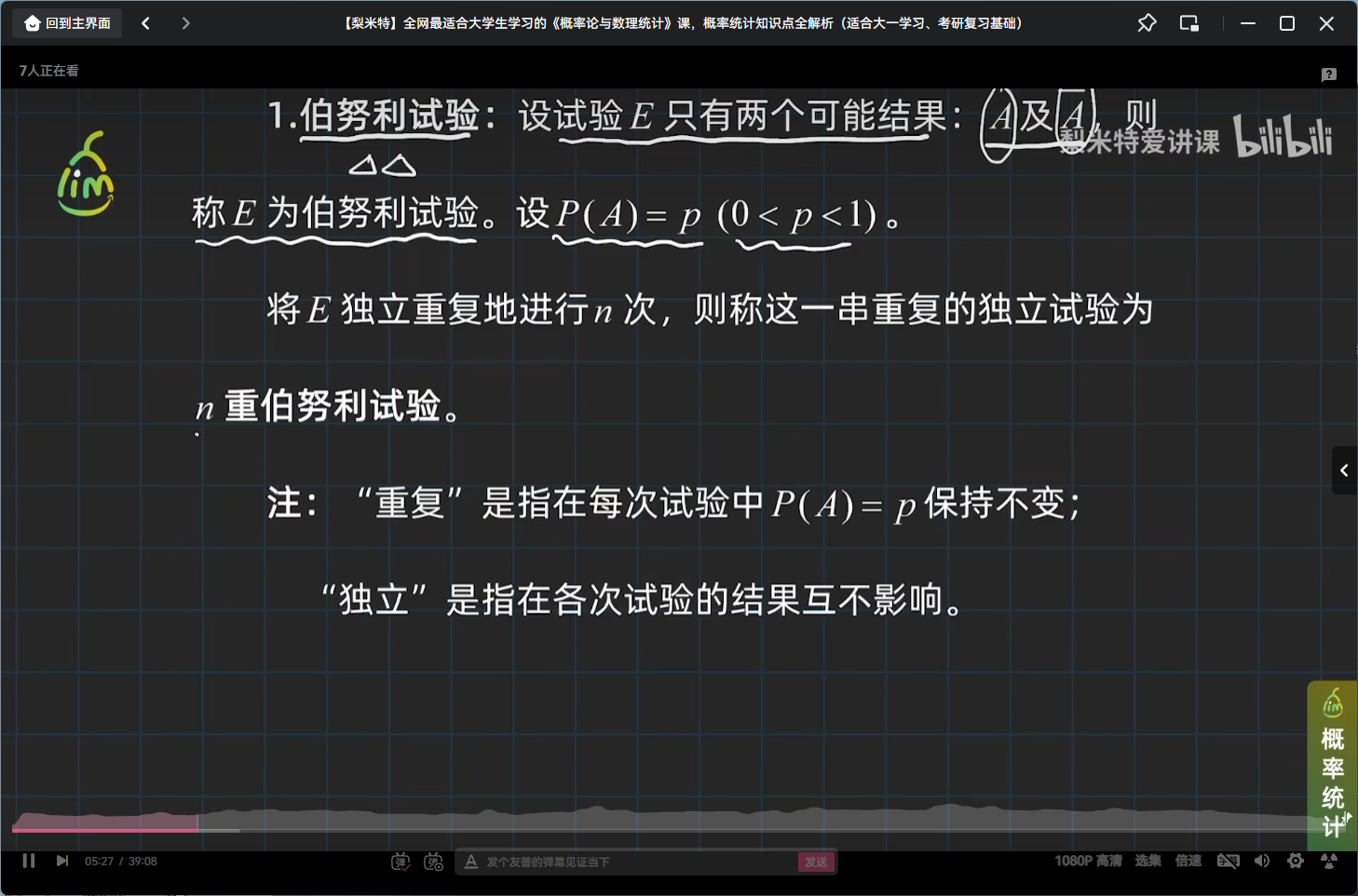
# 最难的离散分布:二项分布
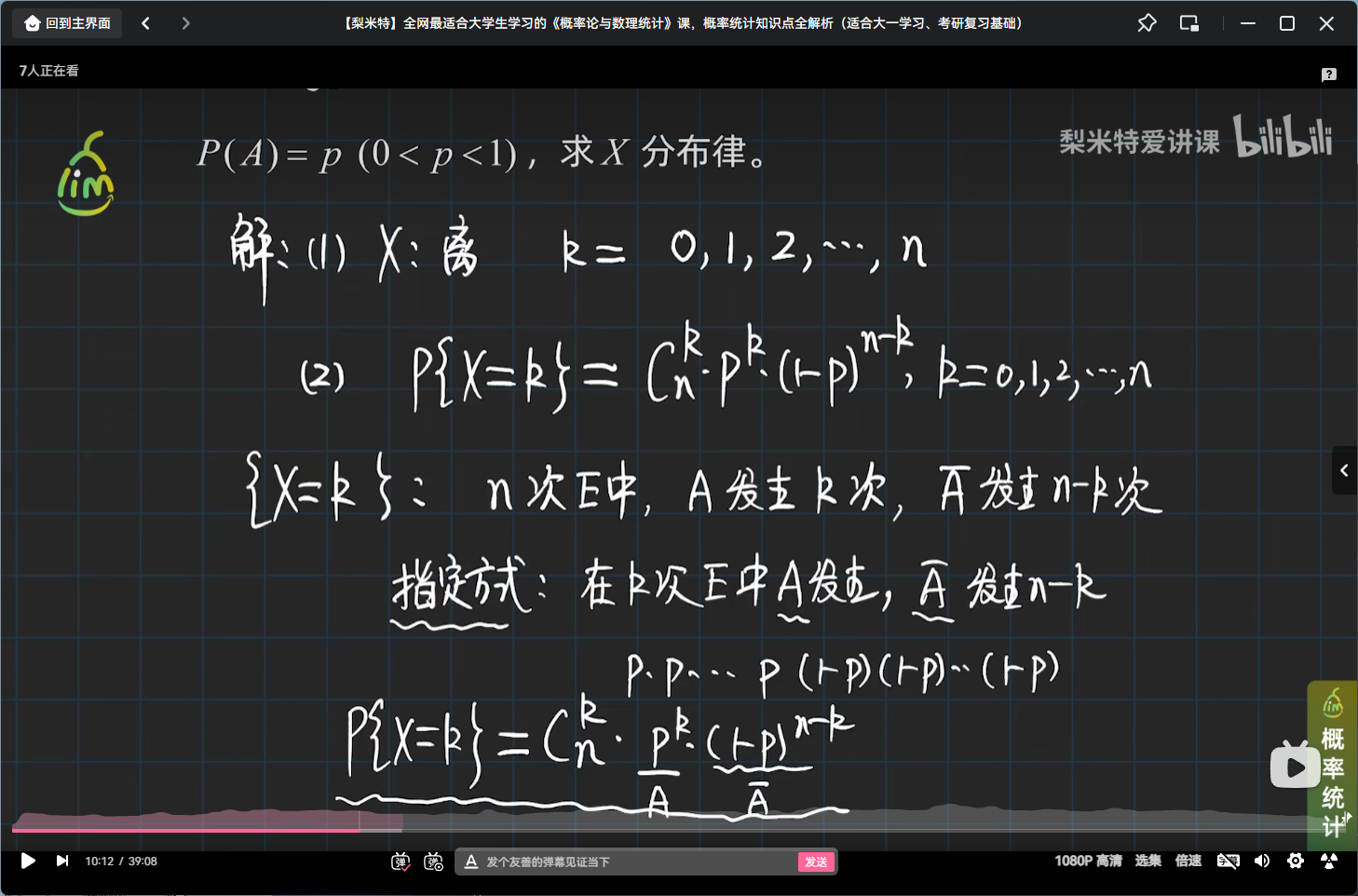
二项分布引例

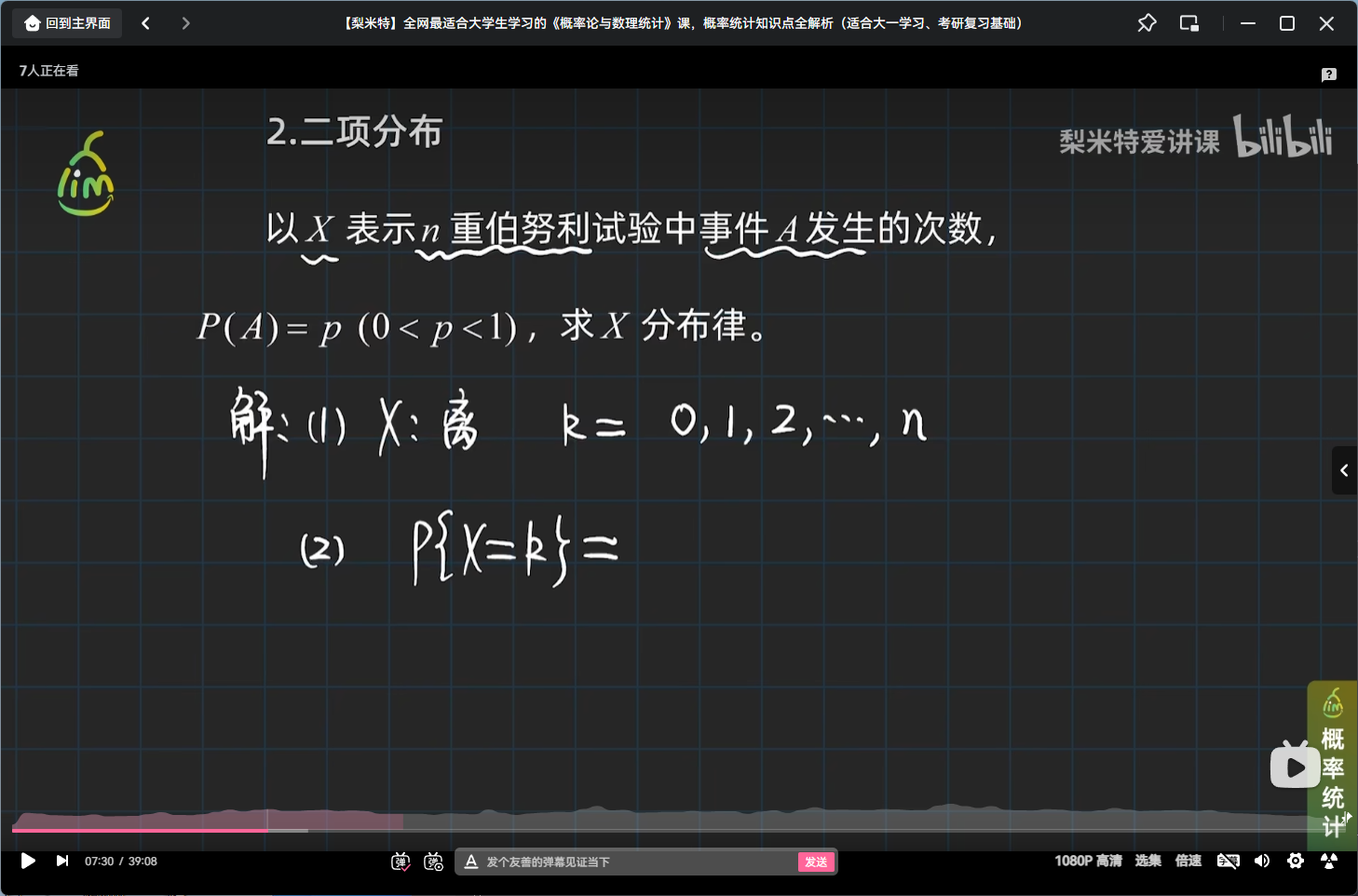
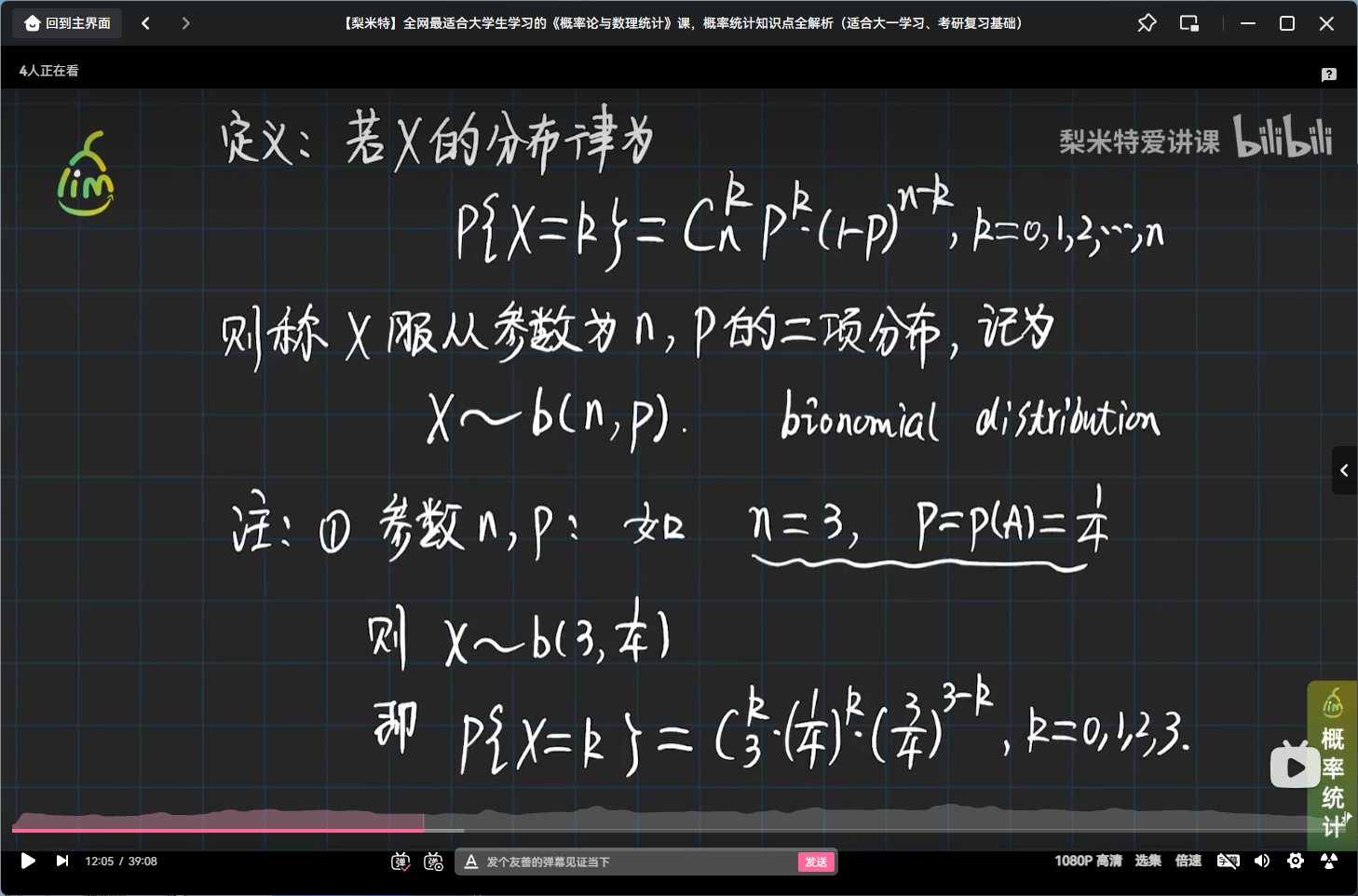
二项分布定义

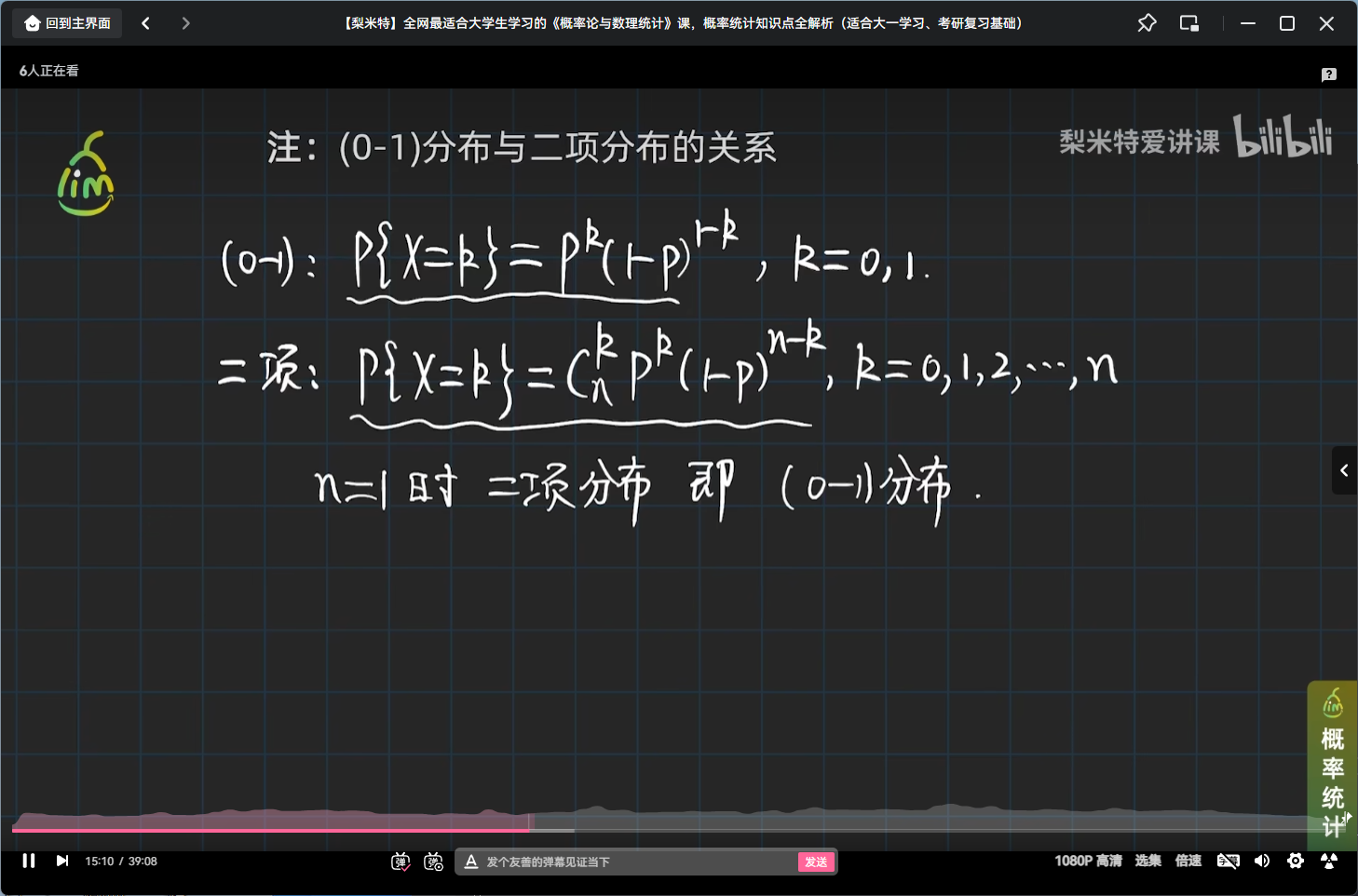
二项分布与0-1分布的关系
二项分布的命名

举个二项分布的栗子



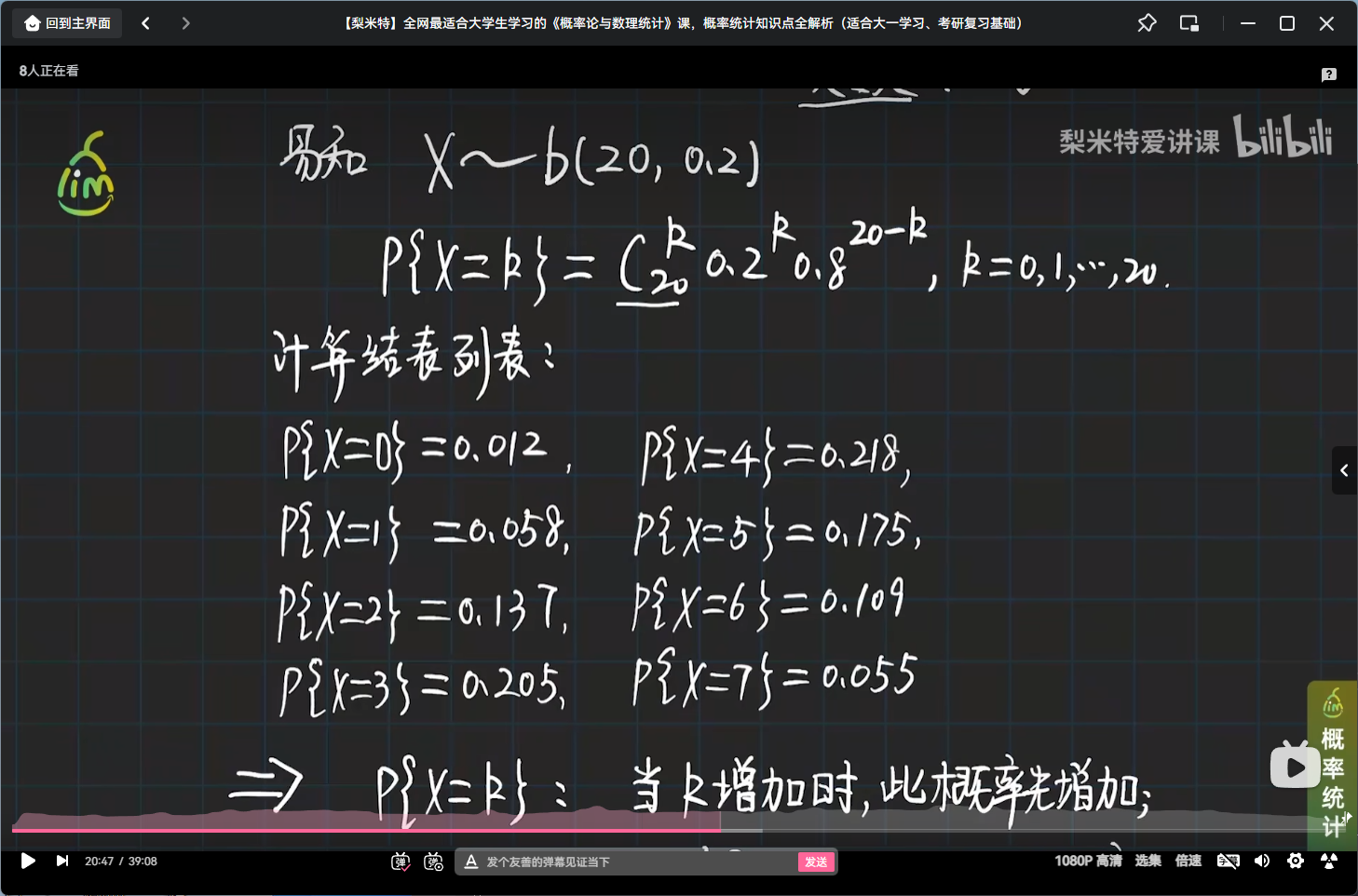
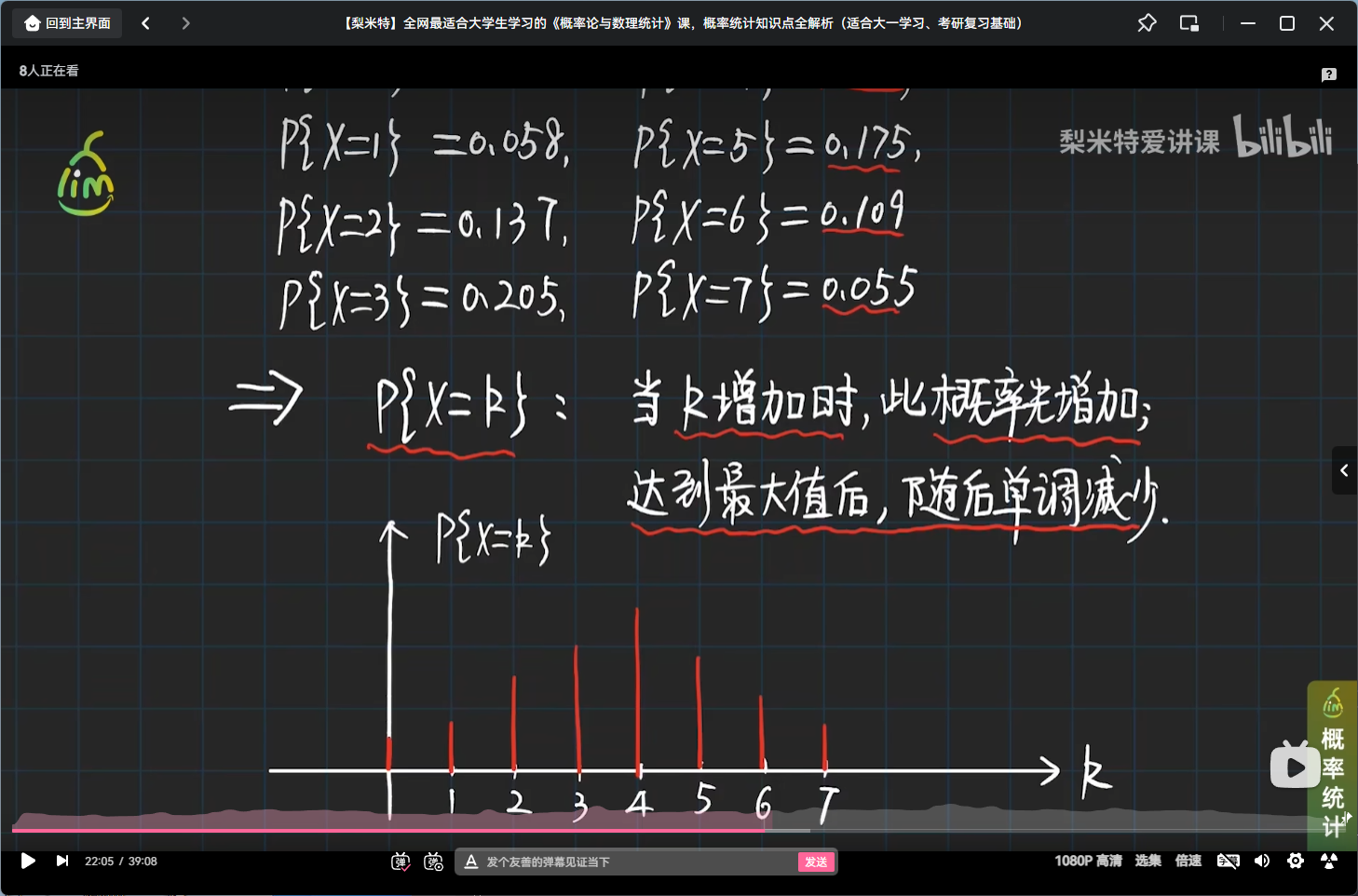
举个二项分布的栗子
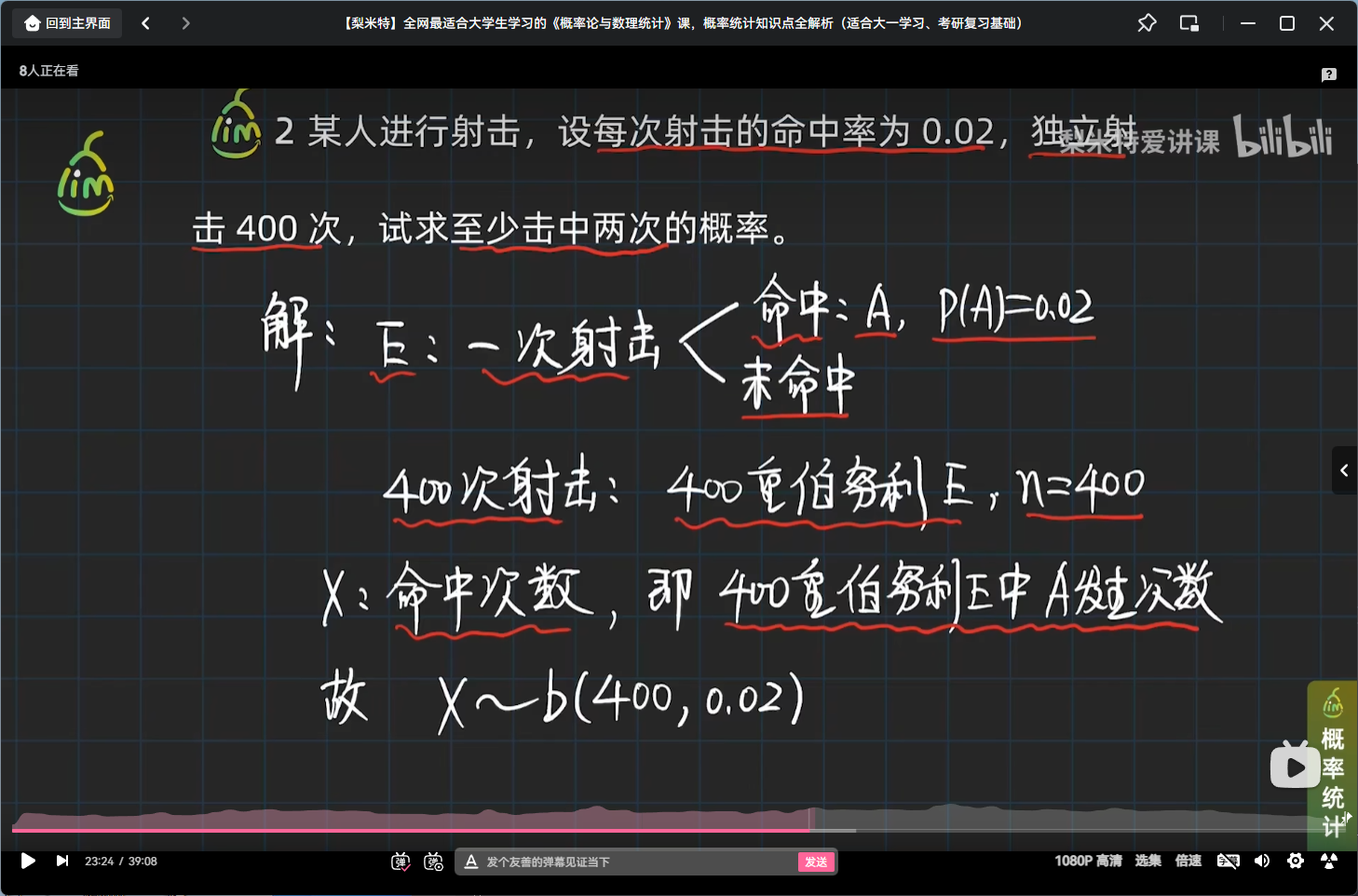
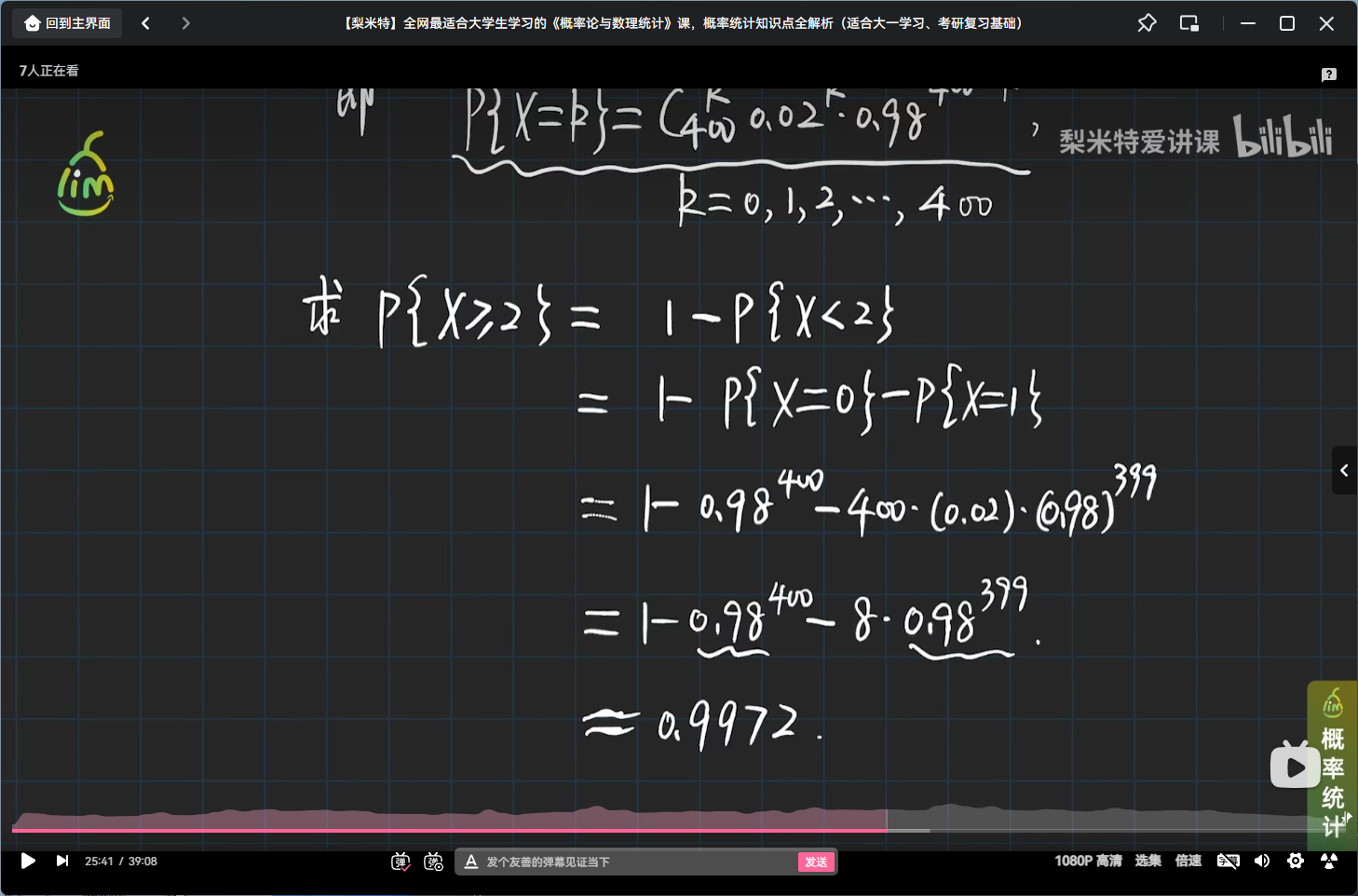

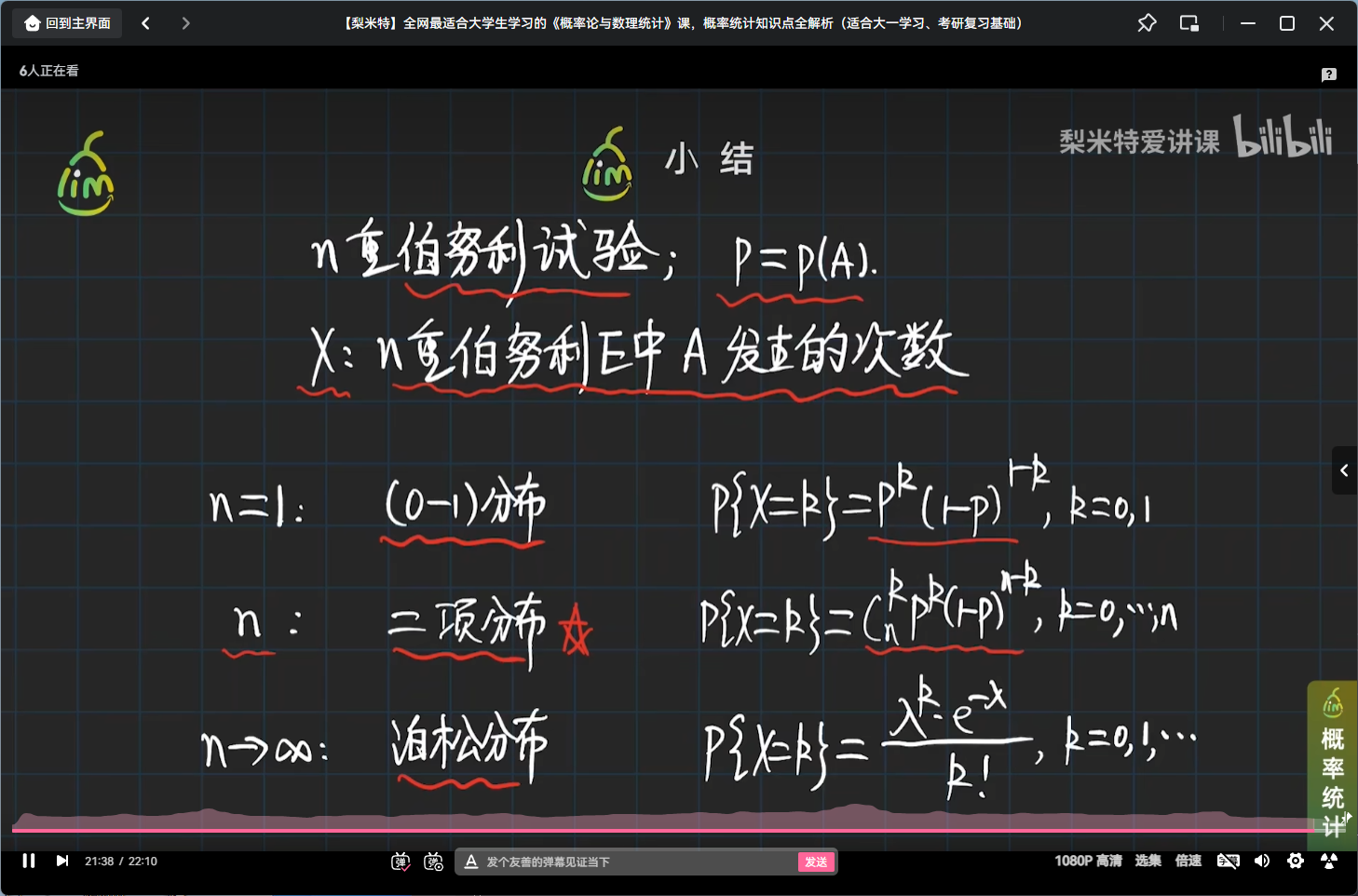
小结
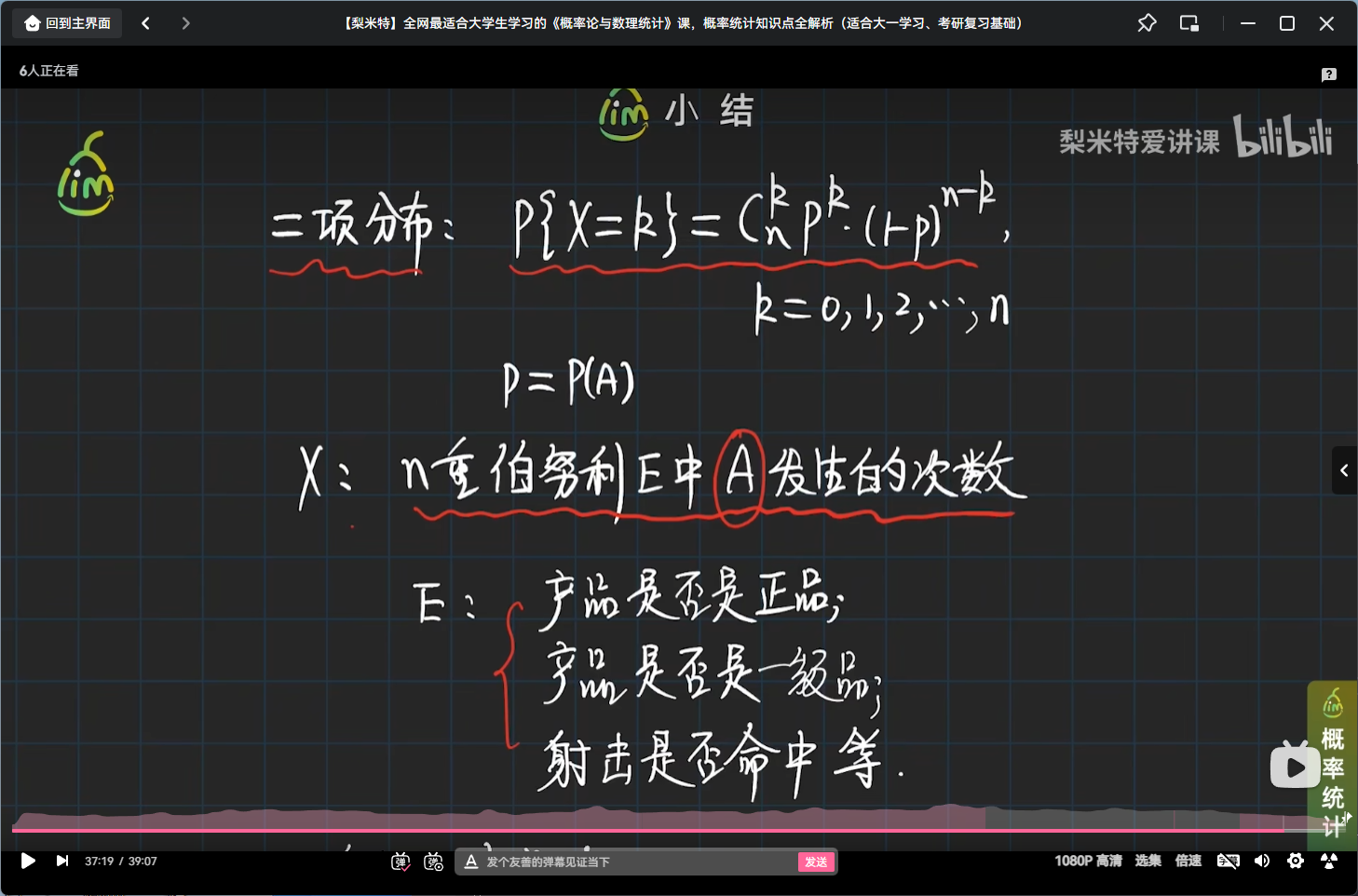

# 泊松分布:n趋于无穷大时的二项分布
泊松分布引例
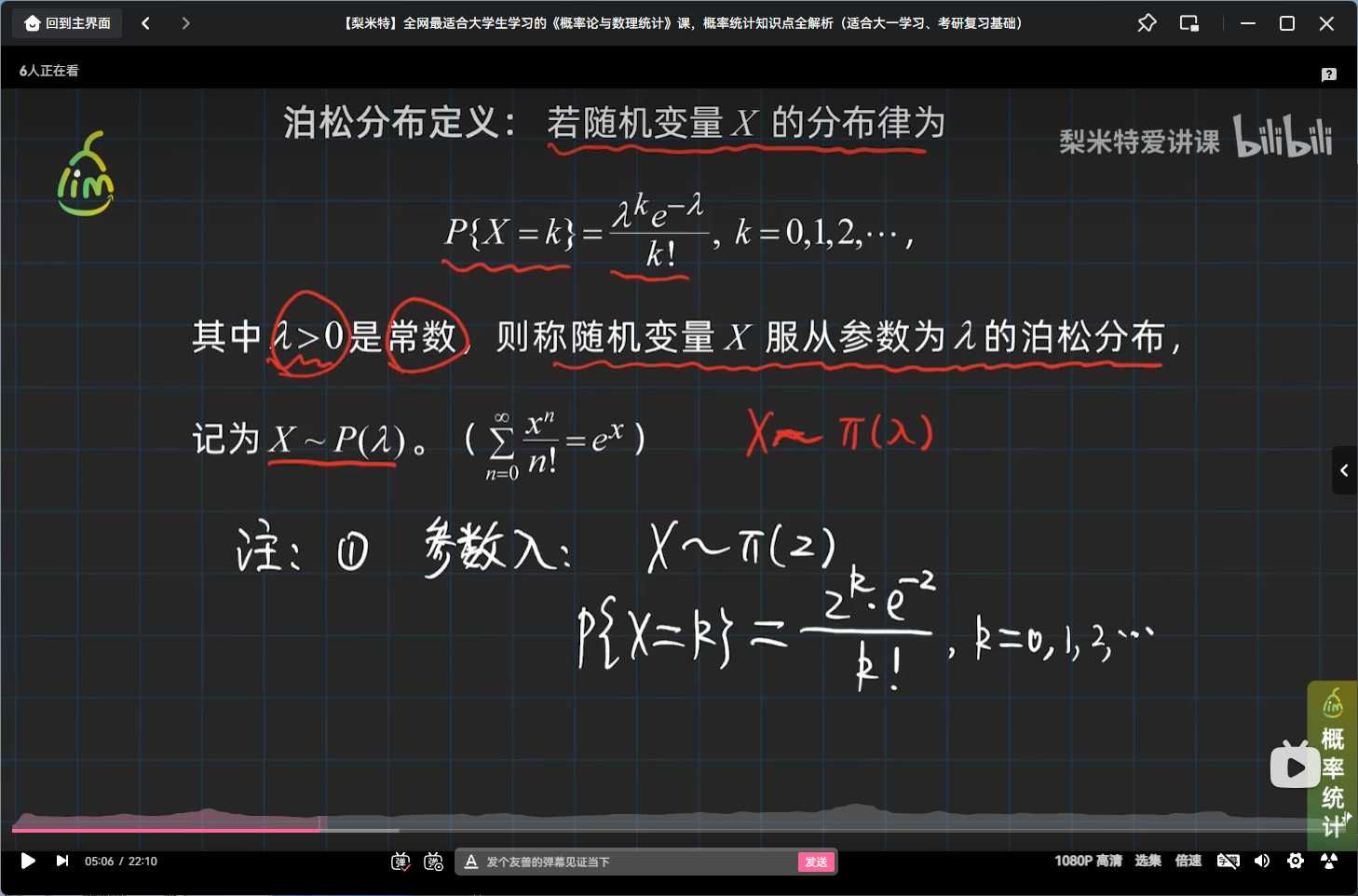
泊松分布定义
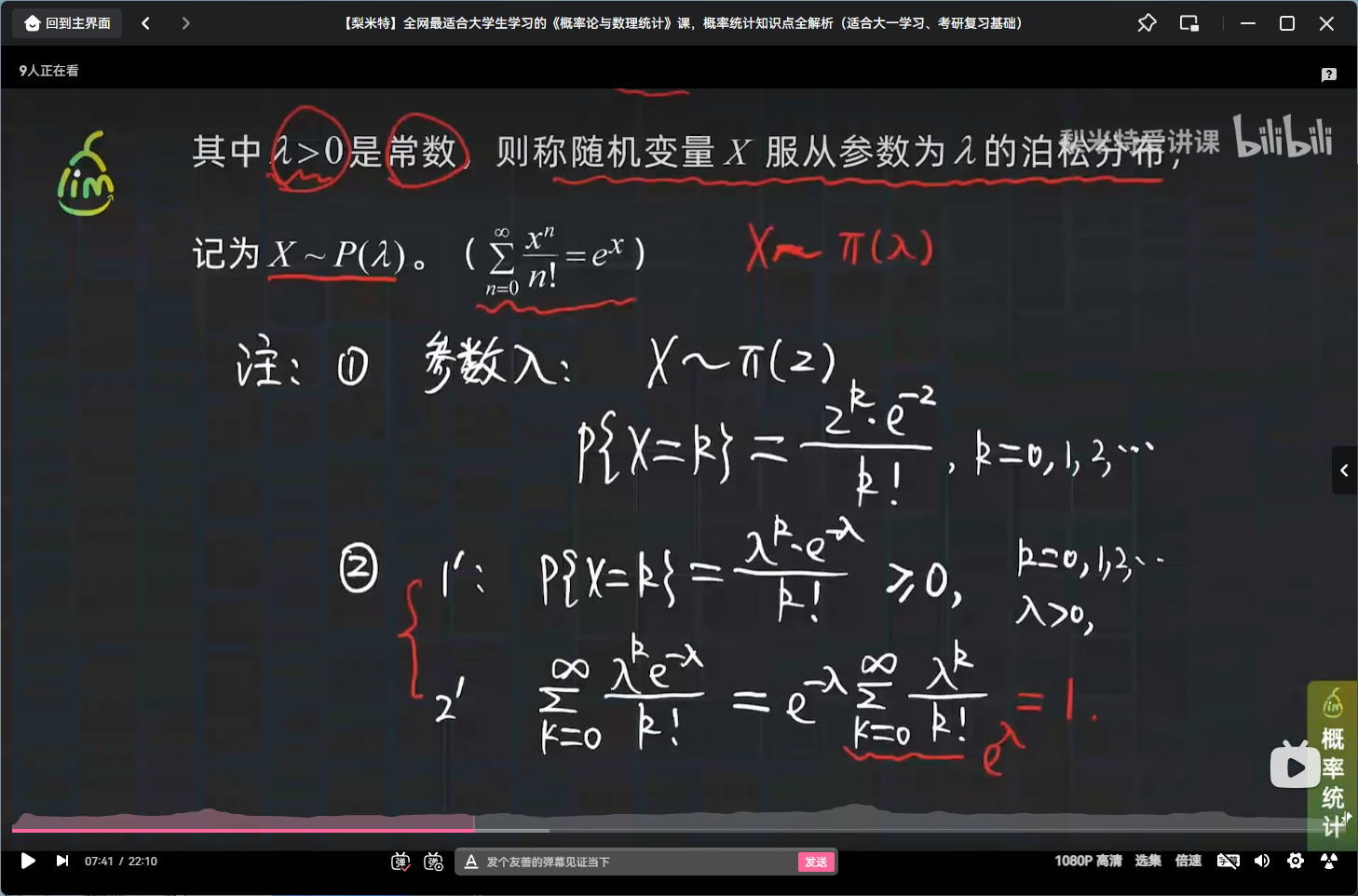
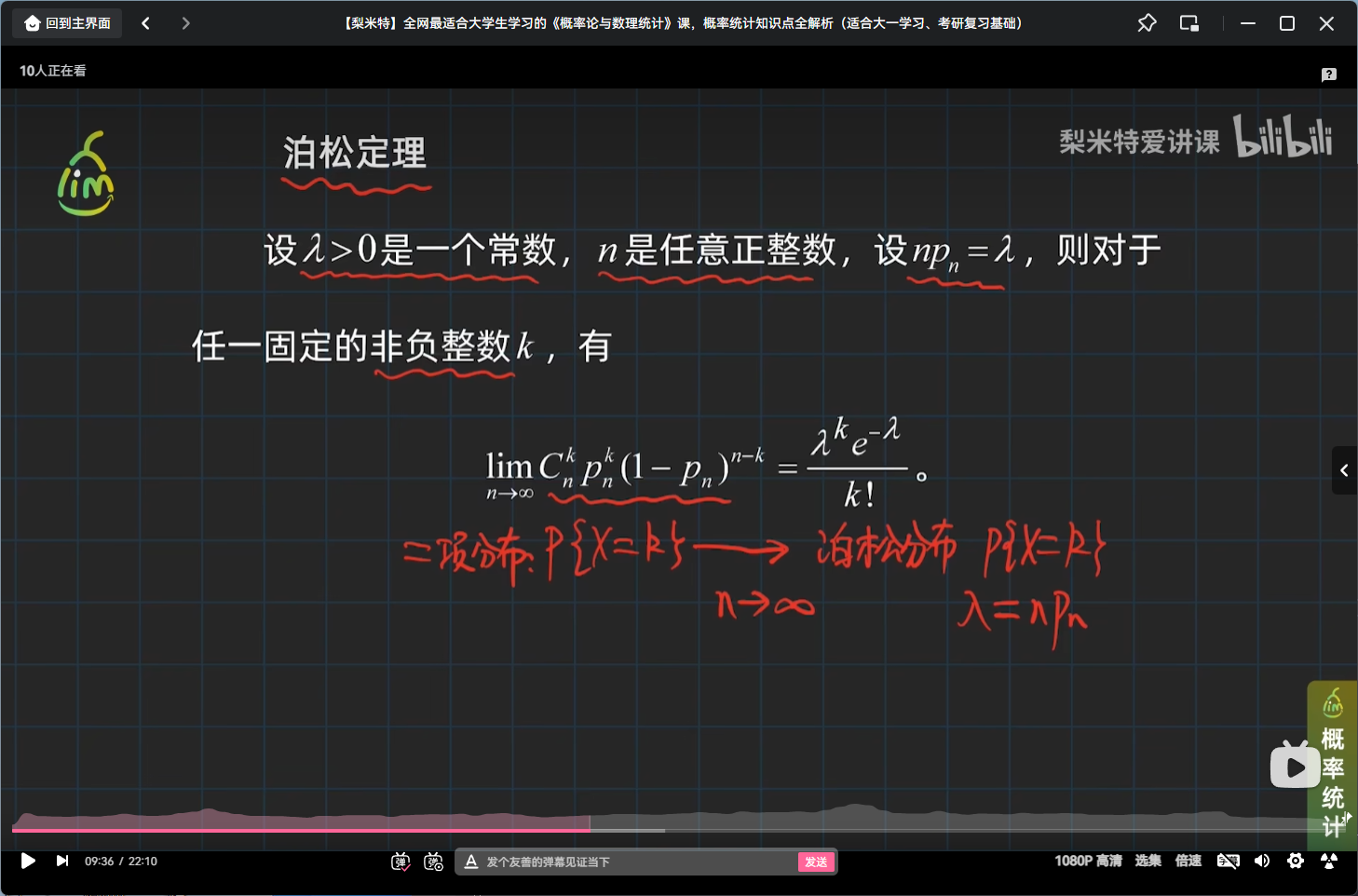
泊松定理
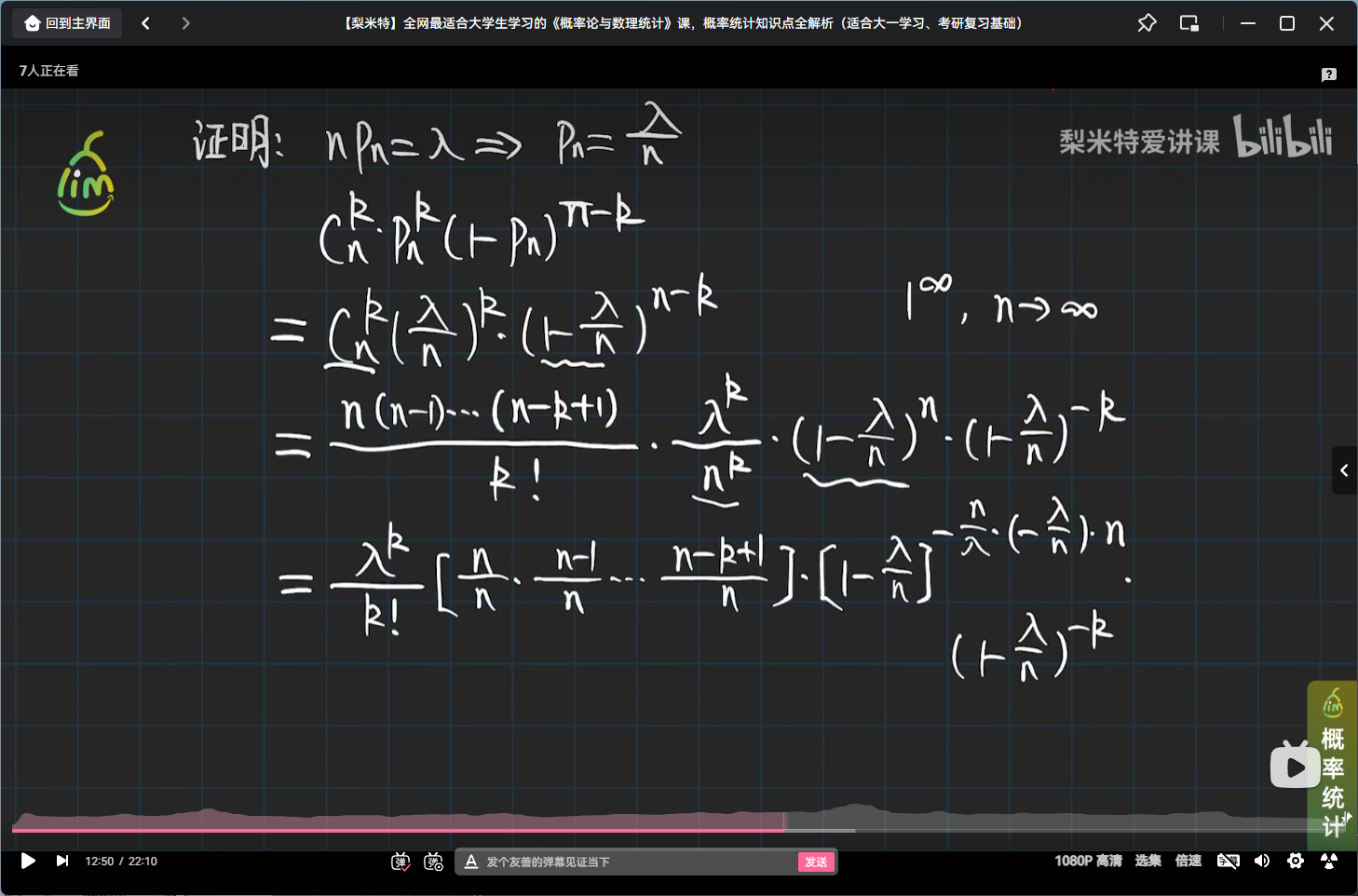
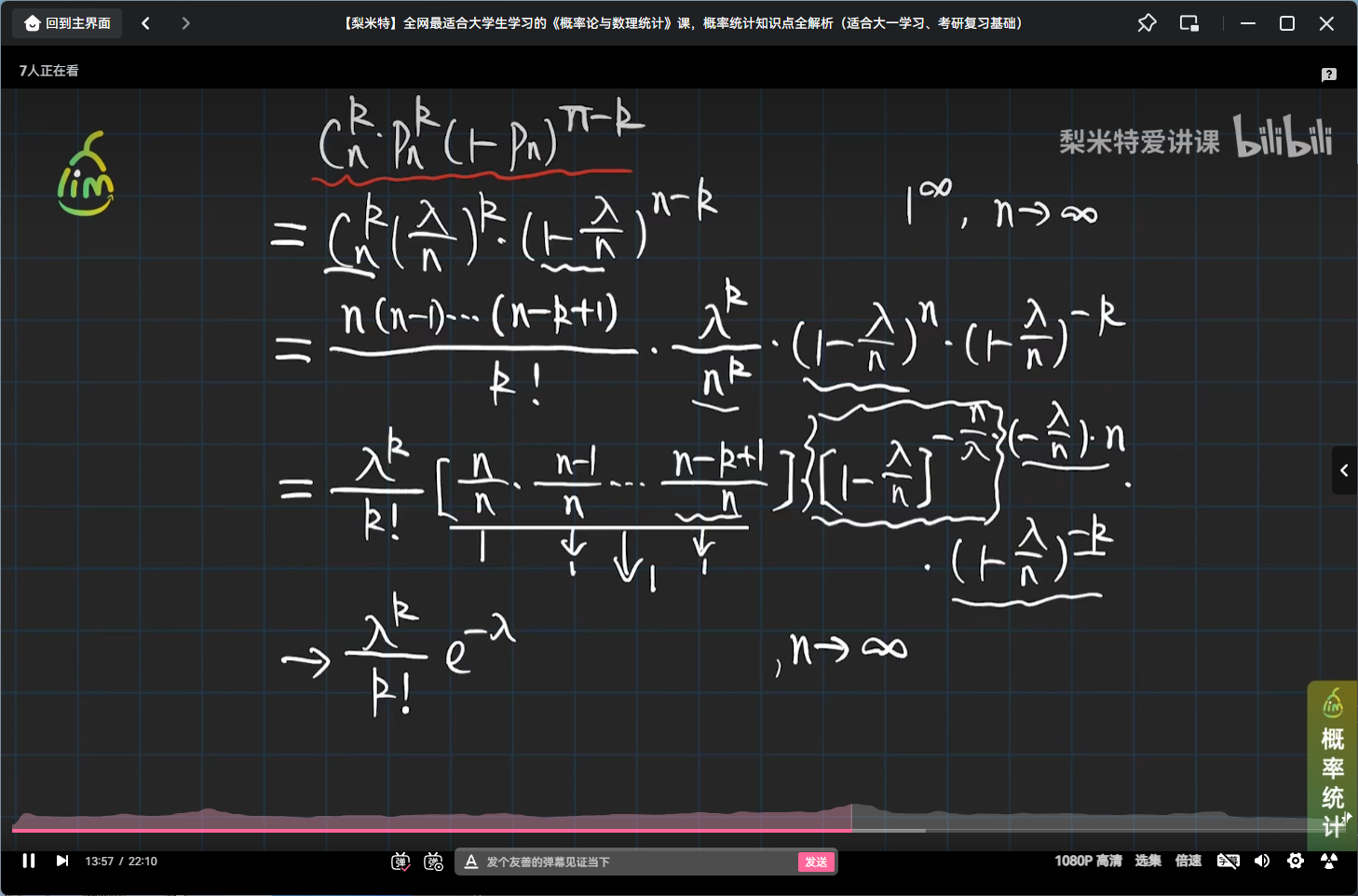
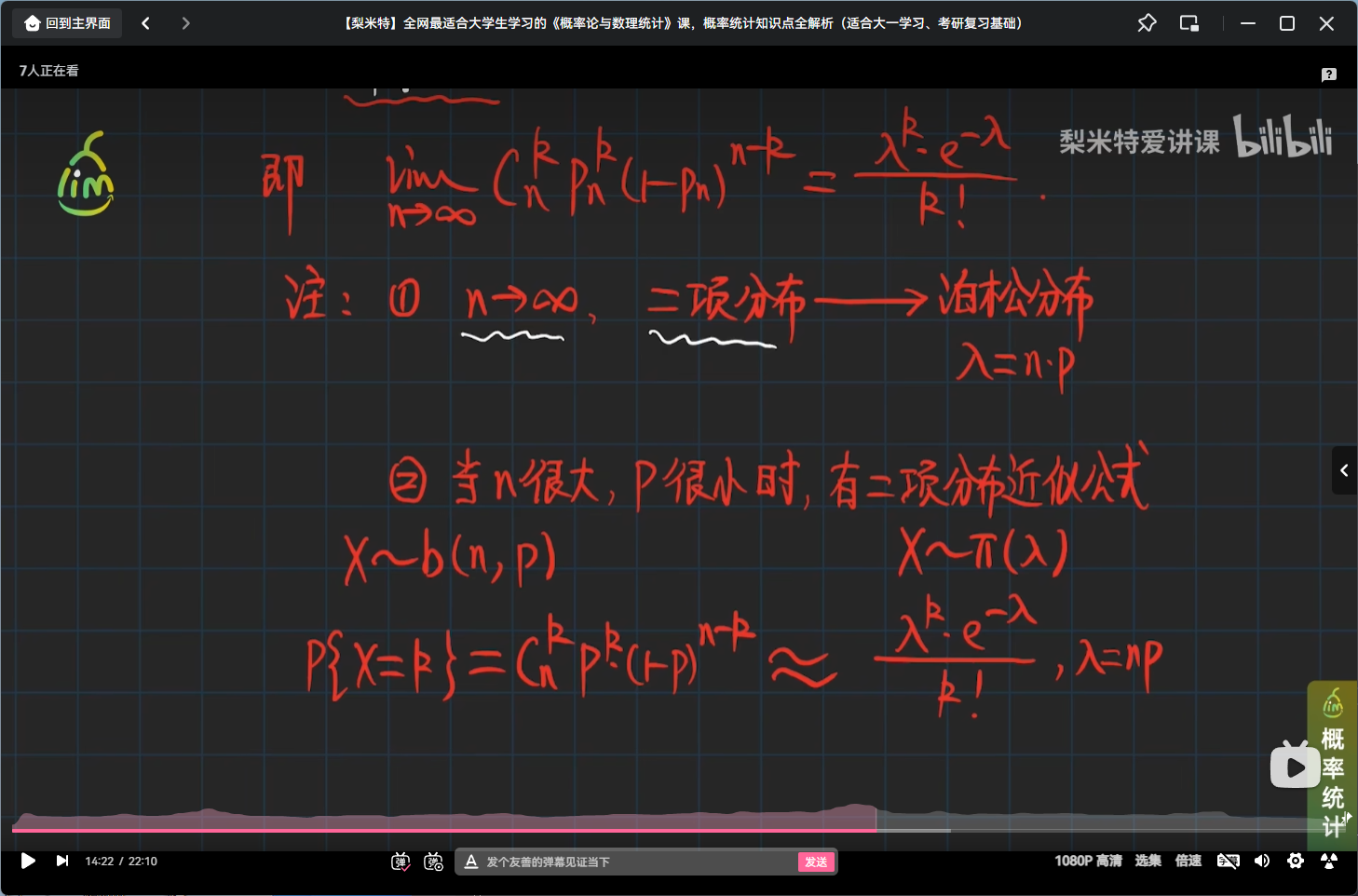
举个泊松分布的栗子
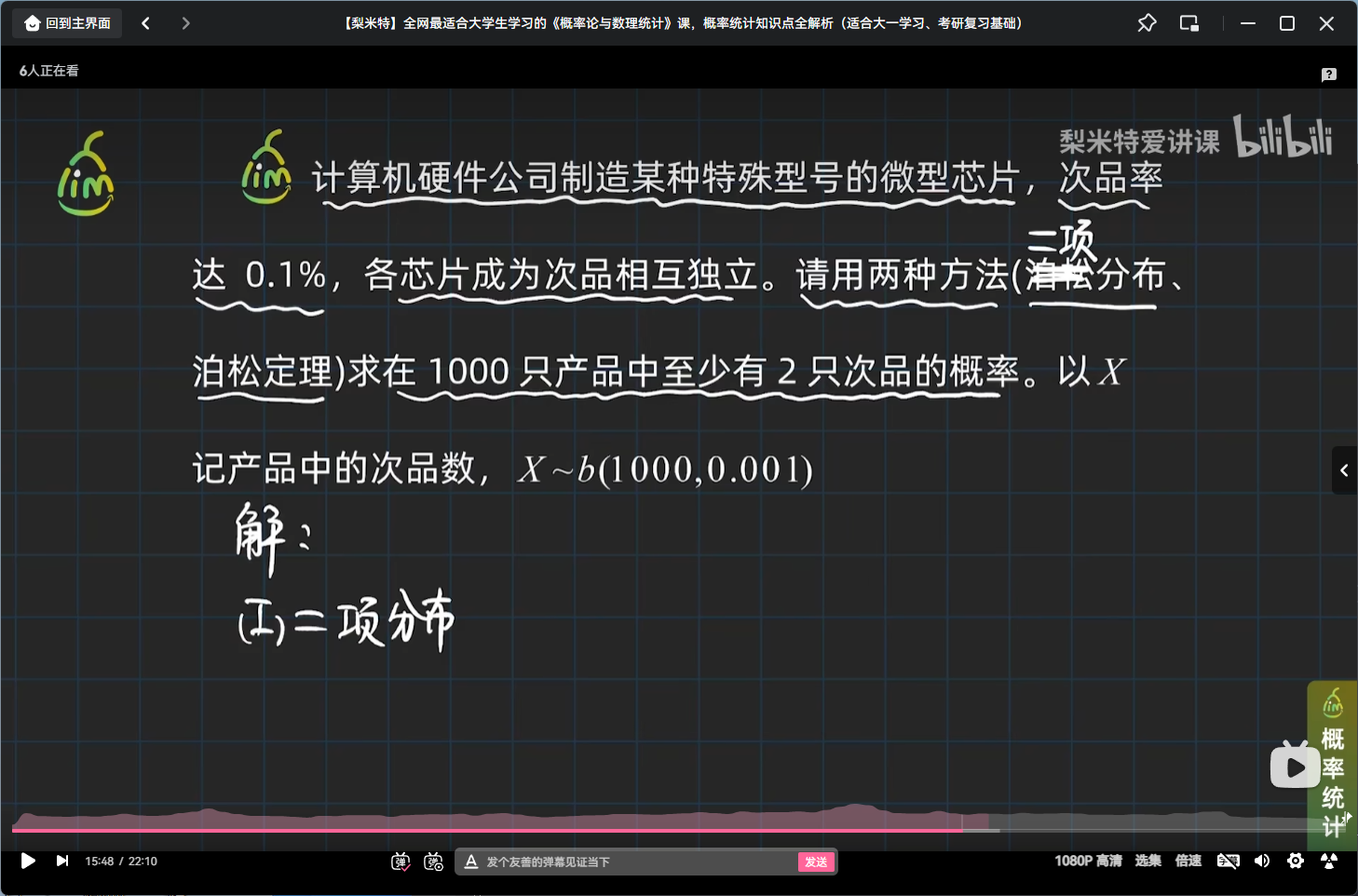
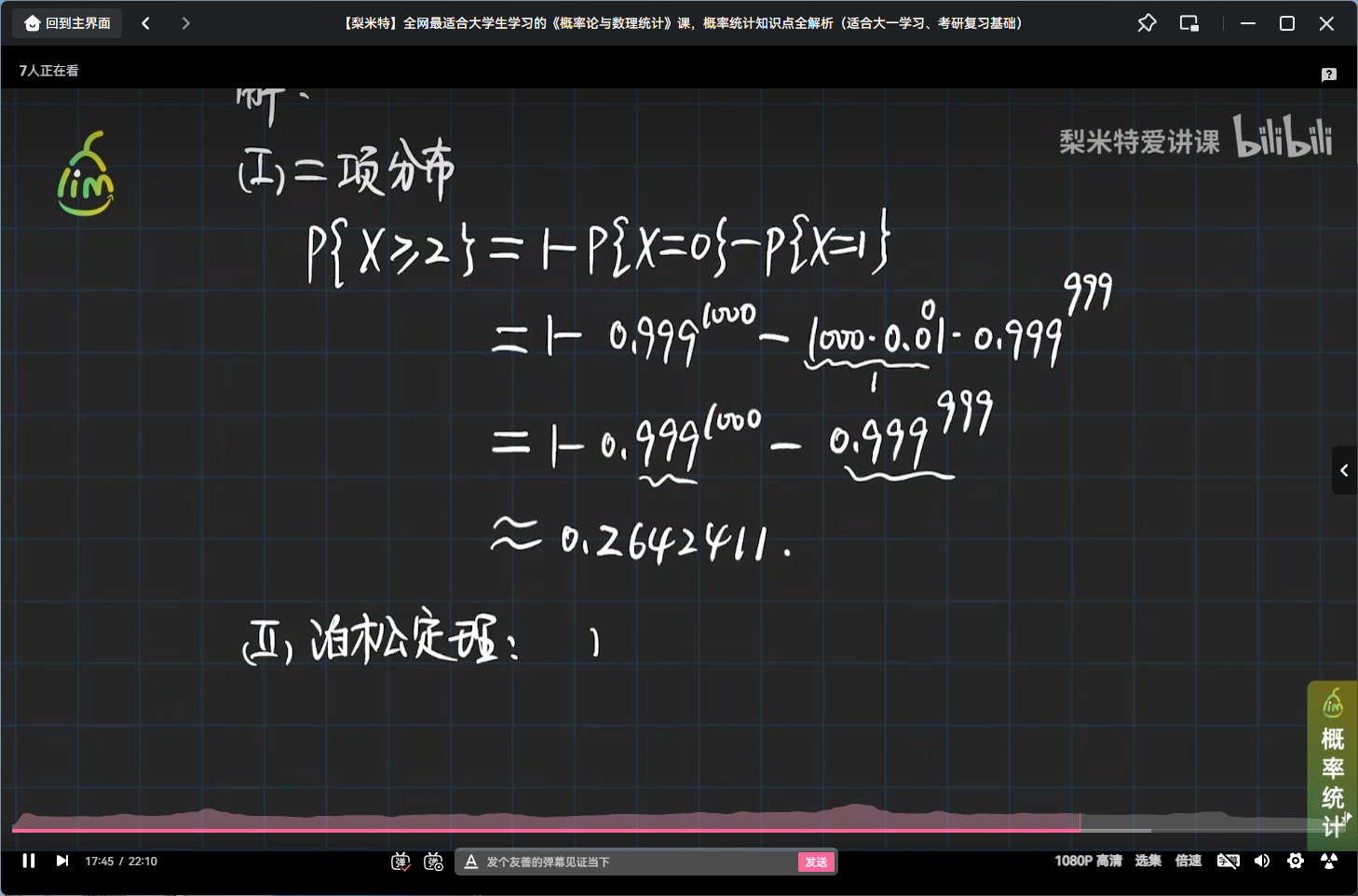
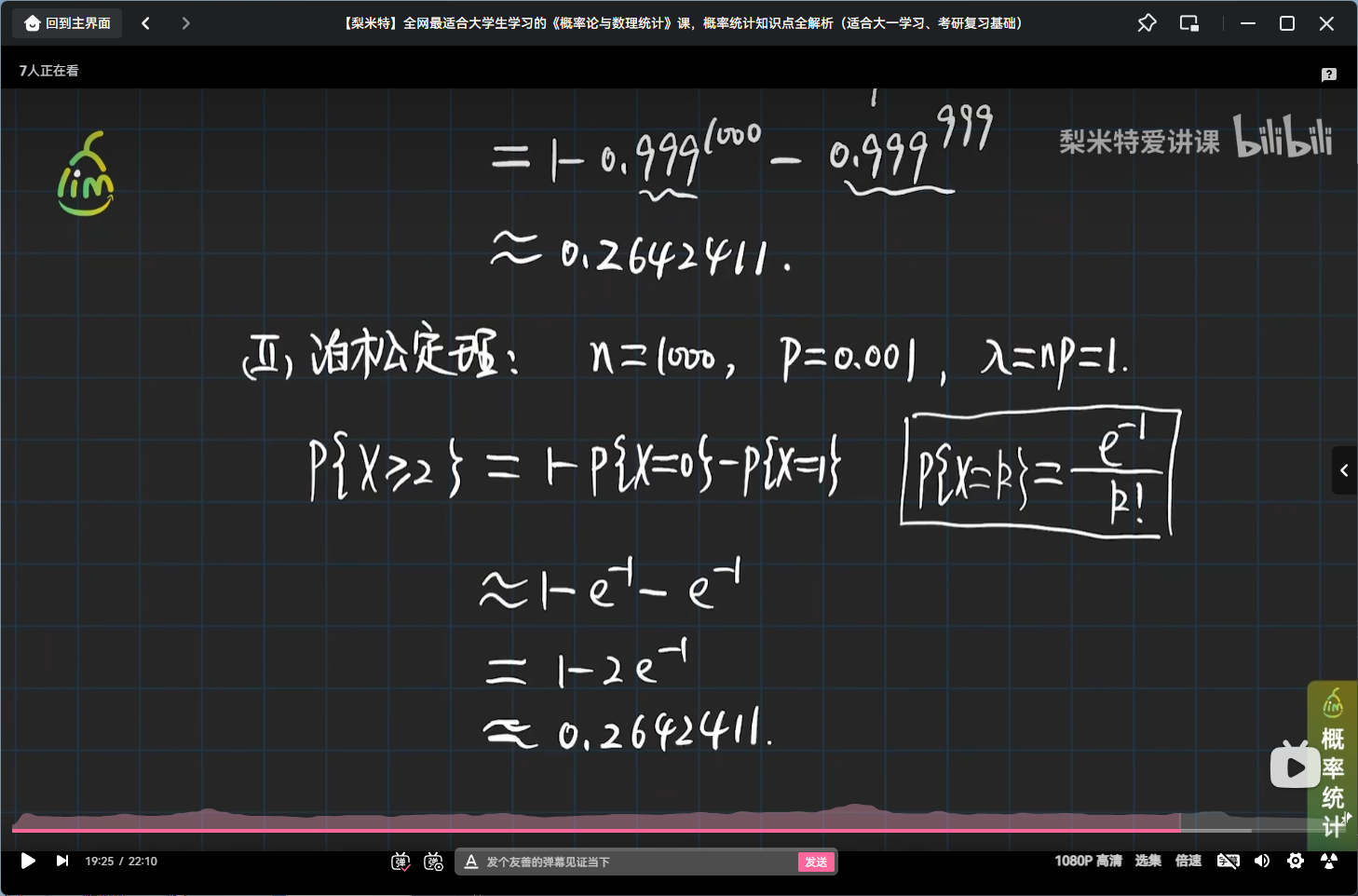
提示
泊松分布也是一种常用的离散型分布,它常常与计数过程相联系,例如:
- 某一时段内某网站的点击量;
- 早高峰时间段内驶入高架道路的车辆数;
- 一本书上的印刷错误数。
小结
# 几何分布
定义
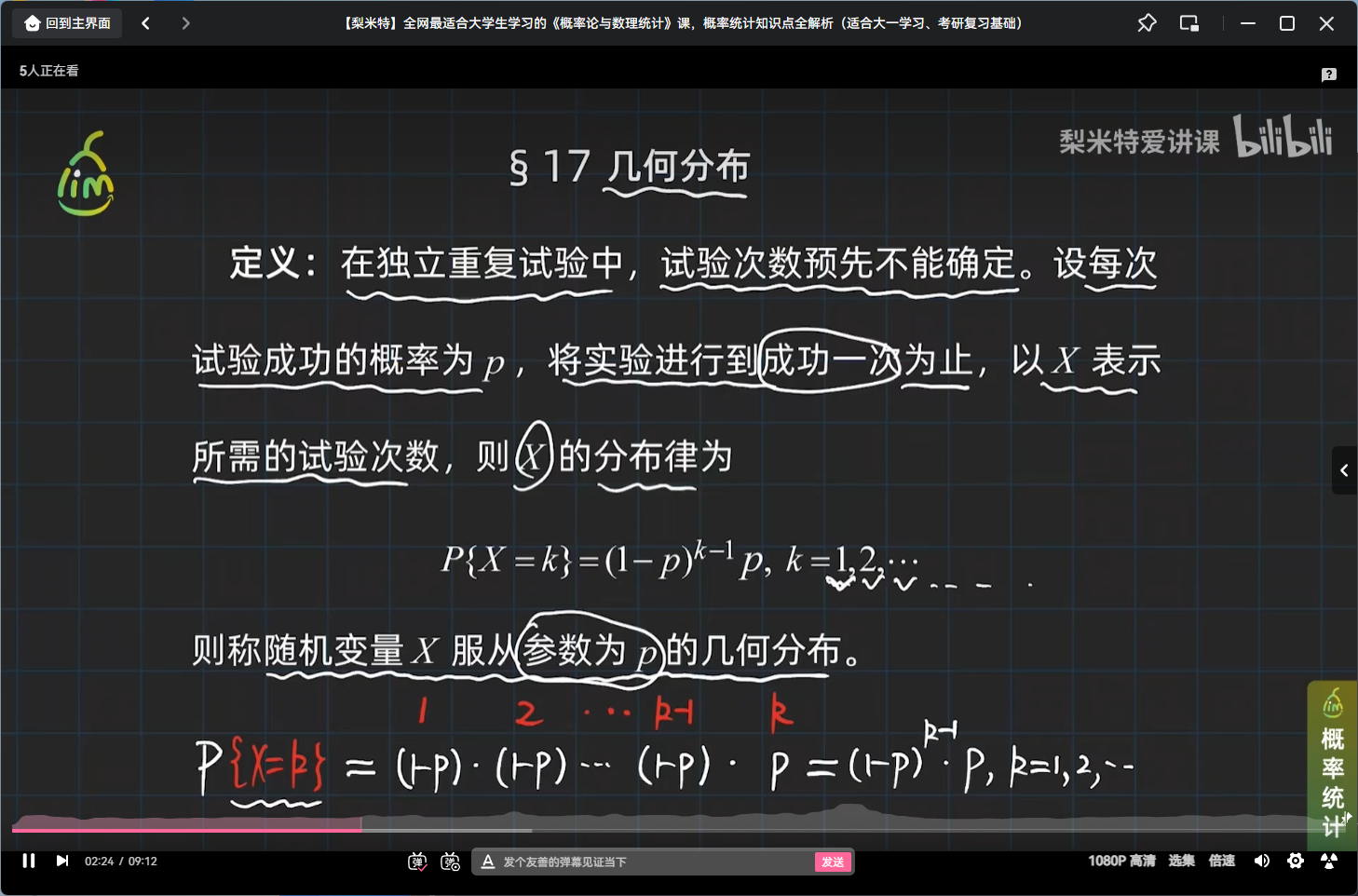
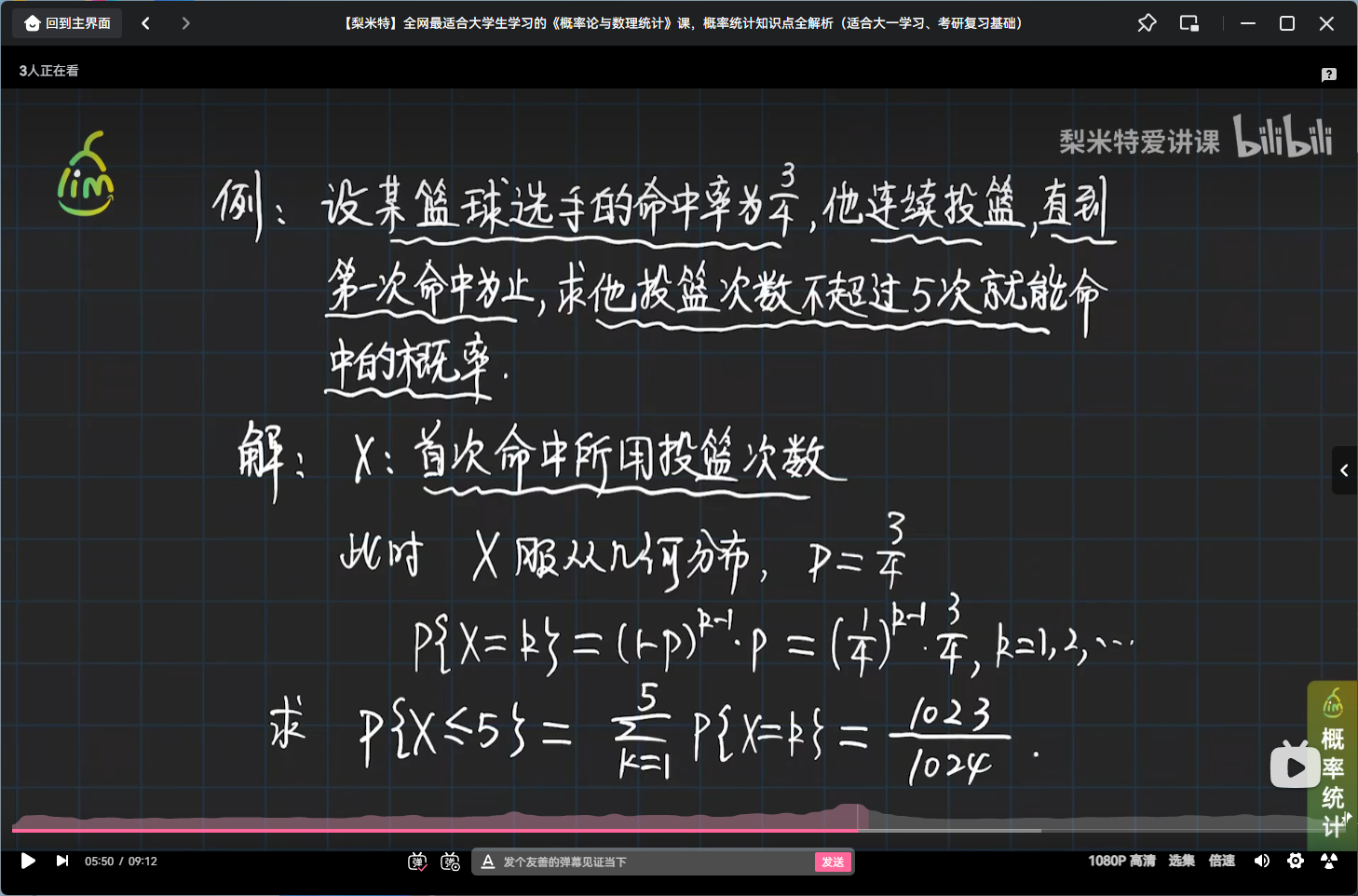
举个几何分布的栗子

# 超几何分布
定义

# 常用的连续型随机变量
# 均匀分布
定义


性质


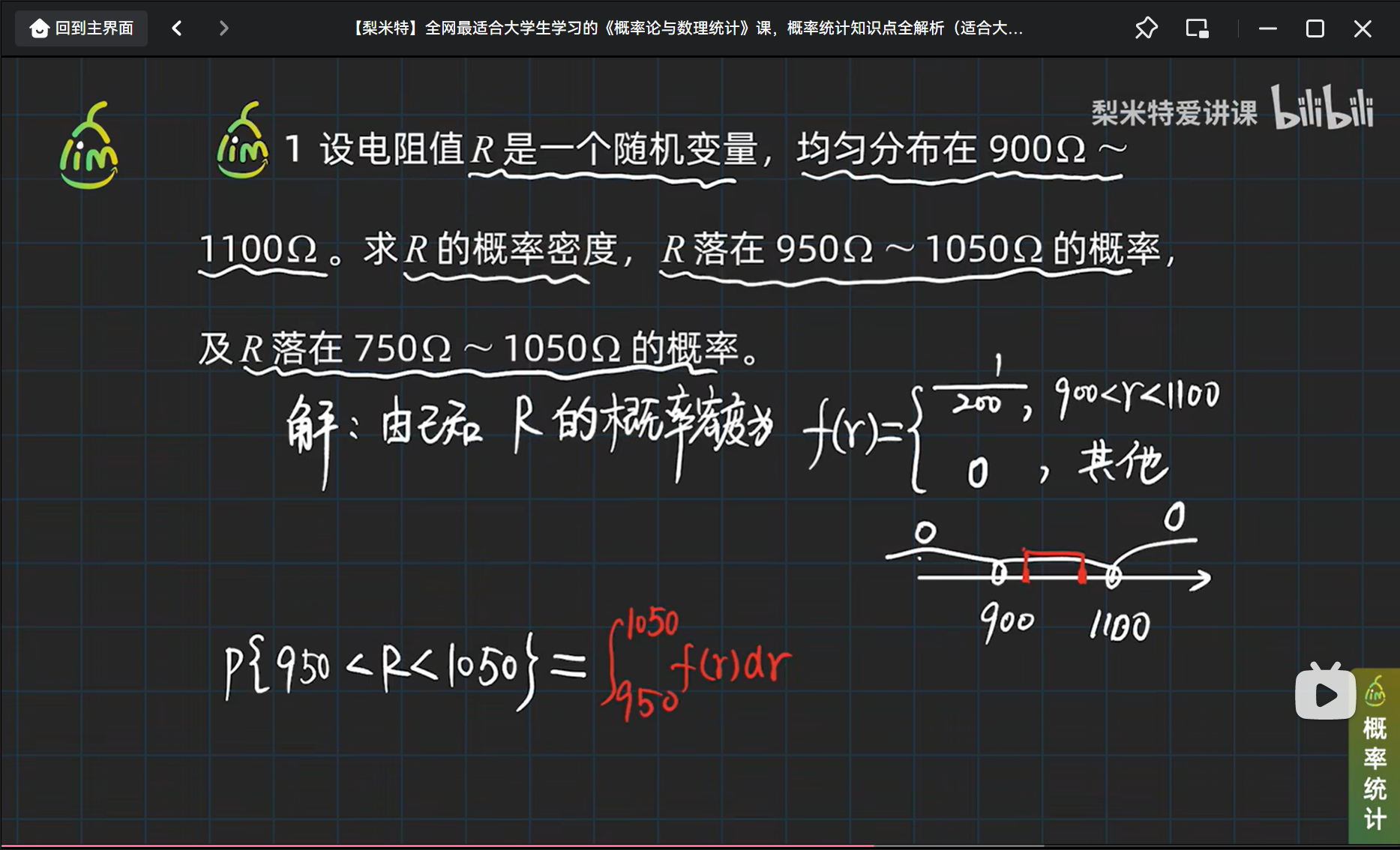
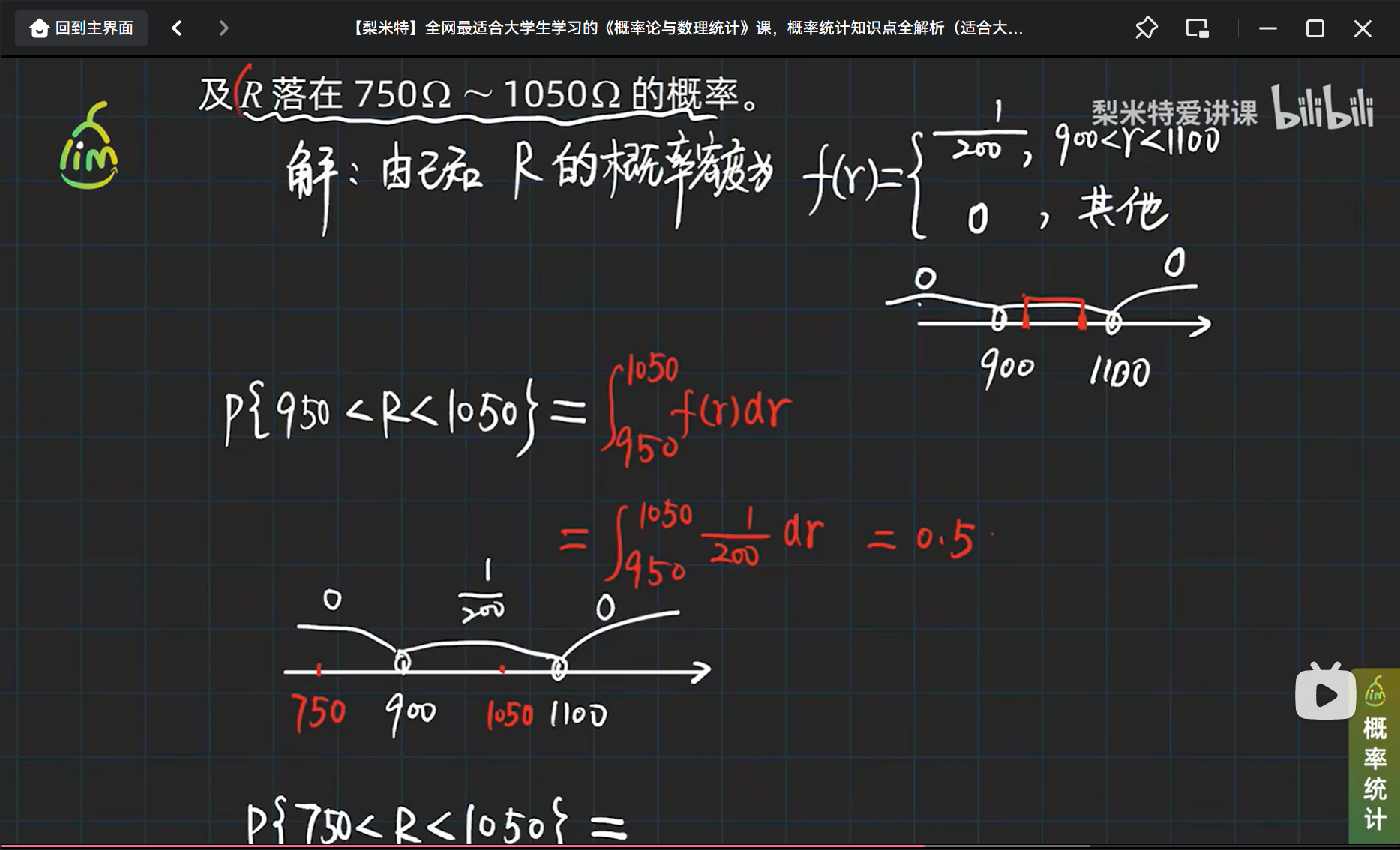
举个均匀分布的栗子

小结 
# 指数分布
定义


性质

# 正态分布:最重要的一种分布
定义

