现实生活当中仅仅用一元随机变量是没有办法来解决的，比如我们要了解学龄儿童的身体发育情况。仅研究身高H和体重W是不够的。我们需要同时考察身高和体重，研究身高和体重之间的关系，这就引入定义在同一样本空间的两个随机变量。

本章主要讨论二维随机变量的（概率）分布，需要高等数学二重积分的知识。二元函数及其二重积分在几何中分别表示曲面以及以该曲面为顶以积分区域为底的曲顶柱体的体积。

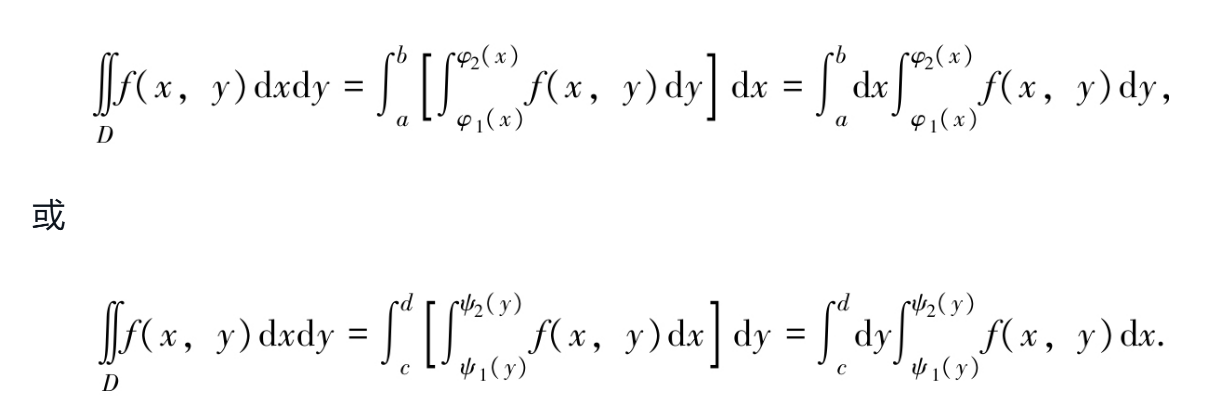
二维随机变量及其联合分布

二维随机变量

定义1　设有随机试验E，其样本空间为Ω。若对Ω中的每一个样本点ω都有一对有序实数（X（ω），Y（ω））与其对应。则称（X，Y）为二维随机变量或二维随机向量。称（X，Y）的取值范围为它的值域，记为Ω（X，Y）。

联合分布函数

对二维随机变量同样要讨论其分布。和一维随机变量有所不同的是，（X，Y）的分布不仅要包含每个随机变量各自的分布信息，还要包含两者之间相互关系的信息。因此称它们的分布为联合分布。首先给出联合分布函数的定义。

二维离散型随机变量及其联合分布律

定义5　如果二维随机变量（X，Y）仅可能取有限个或可列无限个值，则称（X，Y）为二维离散型随机变量。二维离散型随机变量（X，Y）的分布可用联合分布律表示。

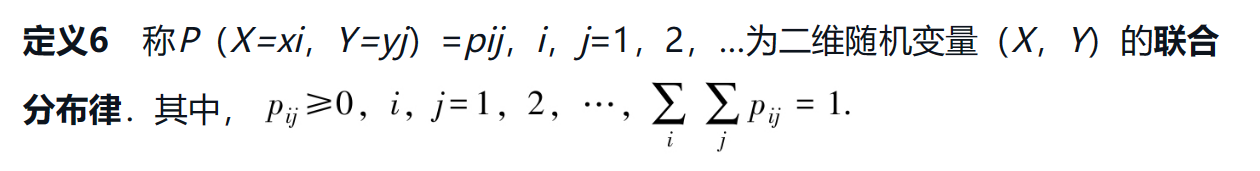
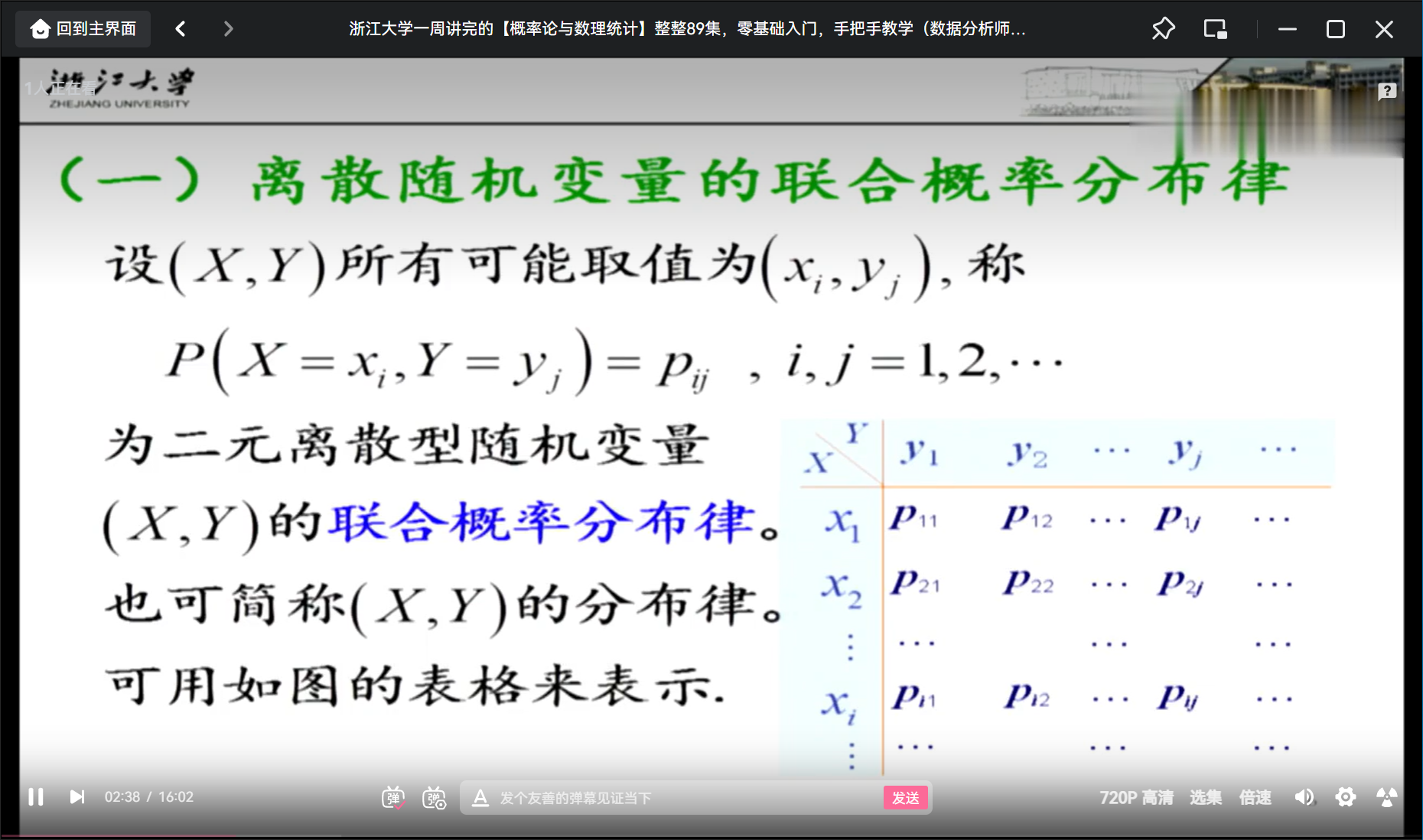
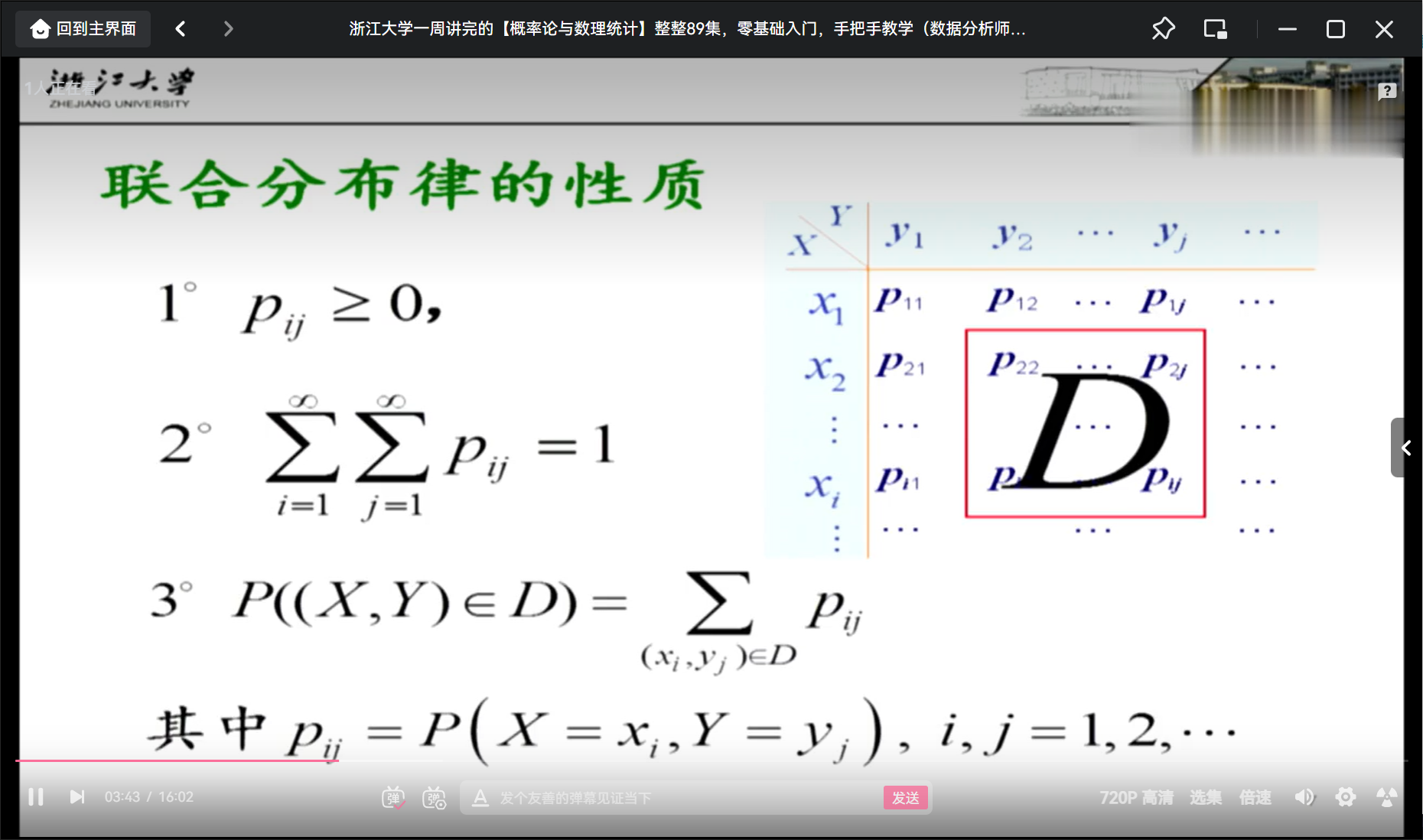
常用的二维随机变量

二维均匀分布