本文来源---周志华机器学习西瓜书(该书建议多次重复阅读)

绪论

引言

人类通过利用经验可以对下次类似情况做出有效的预判和决策。对于机器学习来说，这些经验就是数据。

机器学习正是这样一门学科，它致力于研究如何通过计算的手段，利用经验或者说是数据来改善系统自身的性能。因此，机器学习所研究的主要内容是关于在计算机上从数据中产生"模型 model"的算法，即"学习算法 learning algorithm"。有了学习算法，我们把经验数据提供给它，它就能基于这些数据产生模型。在面对新的测试数据时，模型能为我们作出相应的判断。如果说计算机科学是研究关于"算法 algorithm"的问题，那么类似的，可以说机器学习是研究关于"学习算法 learning algorithm"的问题。

基本术语

经典定义：利用经验改善系统自身的性能。

随着该领域的发展，目前主要研究智能数据分析的理论和方法，并已经成为智能数据分析技术的源泉之一。

要进行机器学习，先要有数据，假定我们收集了一批关于西瓜的数据，例如(色泽=青绿；根蒂=蜷缩；敲声=浊响)，(色泽=乌黑；根蒂=稍蜷；敲声=沉闷)，(色泽=浅白；根蒂=硬挺；敲声=清脆)，...... ，每对括号内是一条记录。这组记录的集合称为一个"数据集dataset"，其中每条记录是关于一个事件或对象(这里是一个西瓜)的描述，称为一个"示例instance"或"样本sample"。反映事件或对象在某方面的表现或性质的事项，如"色泽""根蒂""敲声"，称为"属性attribute"或"特征feature"；属性上的取值，例如"青绿""乌黑"称为"属性值attribute value"。属性构成的空间称为"属性空间attribute space"、"样本空间sample space"或"输入空间"。例如我们把"色泽""根蒂""敲声"作为三个坐标轴，则它们构成一个用于描述西瓜的三维空间，每个西瓜都可在这个空间中找到自己的坐标位置。由于空间中的每个点对应一个坐标向量，因此我们也把一个示例称为一个"特征向量feature vector"。

用符号表示数据集概念如下

从数据中学得模型的过程称为"学习 learning"或"训练 training"，这个过程通过执行某个学习算法来完成。训练过程中使用的数据称为"训练数据 training data"，其中每个样本称为一个"训练样本 training sample"，训练样本组成的集合称为"训练集 training set"。学得模型对应了关于数据的某种潜在规律，因此亦称为"假设 hypothesis"，这种潜在规律自身，则称为"真相"或者"真实 ground truth"，学习过程就是为了找出或者逼近真相。模型有时可称为"学习器 learner"，可以看作学习算法在给定数据和参数空间上的实例化。

如果希望学得一个能帮助我们判断没剖开的是不是"好瓜"的模型，仅有前面的实例数据显然是不够的。要建立这样的关于"预测 prediction"的模型，我们需要获得训练样本的"结果"信息，例如"((色泽=青绿；根蒂=蜷缩；敲声=浊响)，好瓜)。这里关于示例结果的信息，例如"好瓜"，称为"标记 label"，拥有了标记信息的示例，则称为"样例 example"。

用符号表示输出空间或标记空间如下

如果我们欲预测的是离散值，例如"好瓜"，"坏瓜"，此类学习任务称为"分类 classification"，若欲预测的是连续值，例如西瓜成熟度0.95，0.37，此类学习任务称为"回归 regression"。对只涉及两个类别的"二分类 binary classification"任务，通常称其中一个类为"正类 positive class"，另一个为"反类 negative class"；涉及多个类别时，则称为"多分类 multi-class classification"任务。

用符号表示二分类或多分类如下

学得模型后，使用其进行预测的过程称为"测试 testing"，被预测的样本称为"测试样本 testing sample"。

我们还可以对西瓜做"聚类 clustering"，即将训练集中的西瓜分成若干组，每组称为一个"簇 cluster"。这些自动形成的簇可能对应一些潜在的概念划分，例如"浅西瓜""深西瓜"，甚至是"本地瓜""外地瓜"。这样的学习过程有助于我们了解数据内在的规律，能为更深入地分析数据建立基础。需要说明的是，在聚类学习中，"浅西瓜""深西瓜""本地瓜"这样的概念我们事先是不知道的，而且学习过程中使用的训练样本通常不拥有标记信息。

根据训练数据是否拥有标记信息，学习任务可大致划分为两大类"监督学习 supervised learning"和"无监督学习 unsupervised learning"。分类和回归是有监督学习代表，聚类则是无监督学习代表。

需要注意的是，机器学习的目标是使学得的模型能很好地适用于"新样本"，而不仅仅在训练样本上工作得很好。即便对聚类这样的无监督学习任务，我们也希望学得的簇划分能适用于没在训练集中体现的样本。学得模型适用于新样本的能力，称为"泛化 generalization"能力。具有强泛化能力的模型能很好地适用于整个样本空间。于是，尽管训练集通常只是样本空间的一个很小的采样，我们仍希望它能很好地反映出样本空间的特性，否则就很难期望在训练集上学得的模型能在整个样本空间上都工作的很好。

假设空间

归纳 induction与演绎 deduction是科学推理的两大基本手段。前者是从特殊到一般的"泛化 generalization"过程，即从具体的事实归纳出一般性规律。后者则是从一般到特殊的"特化 specialization"过程，即从基础原理推演出具体状况。例如在数学公理系统中，基于一组公理和推理规则推导出与之相恰的定理，这是演绎。而从样本例中学习，显然是一个归纳的过程，因此亦称"归纳学习 inductive learning"。

归纳学习有狭义与广义之分，广义的归纳学习大体相当于从样例中学习，而狭义的归纳学习则要求从训练数据中学得"概念 concept"，因此亦称为"概念学习"或"概念形成"概念学习技术目前研究、应用都比较少，因为要学得泛化性能好且语义明确的概念实在太困难了，现实常用的技术大多是产生"黑箱"模型。然而对概念学习有所了解，有助于理解机器学习的一些基础思想。

概念学习中最基本的是布尔概念学习，即对"是""不是"这样的可表示为0/1布尔值的目标概念的学习。

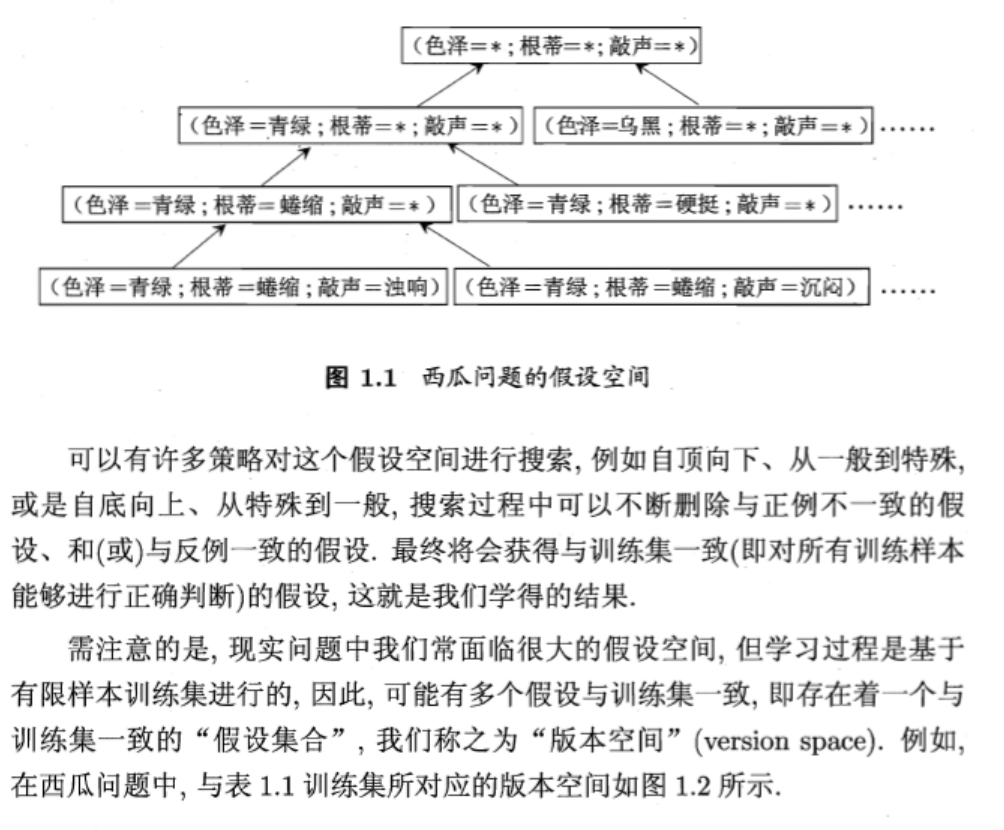
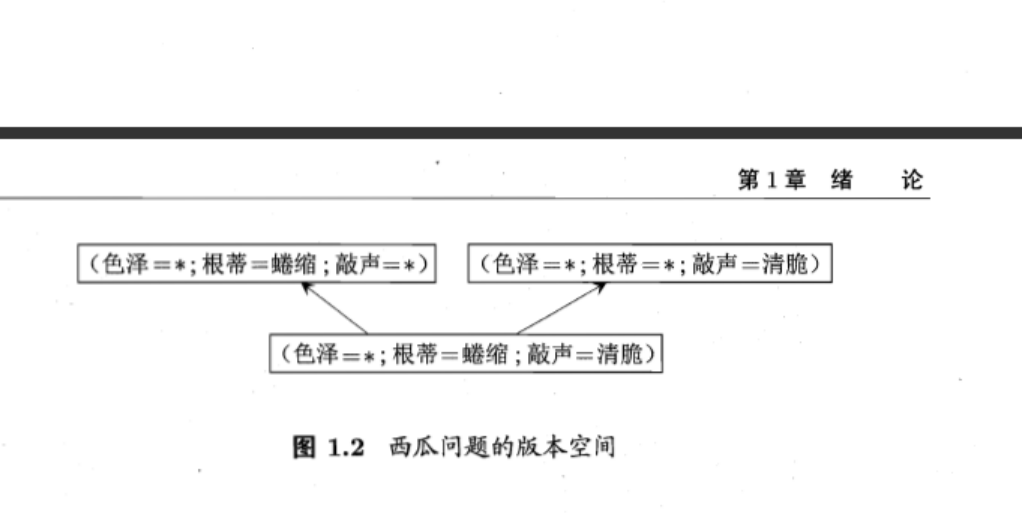
归纳偏好

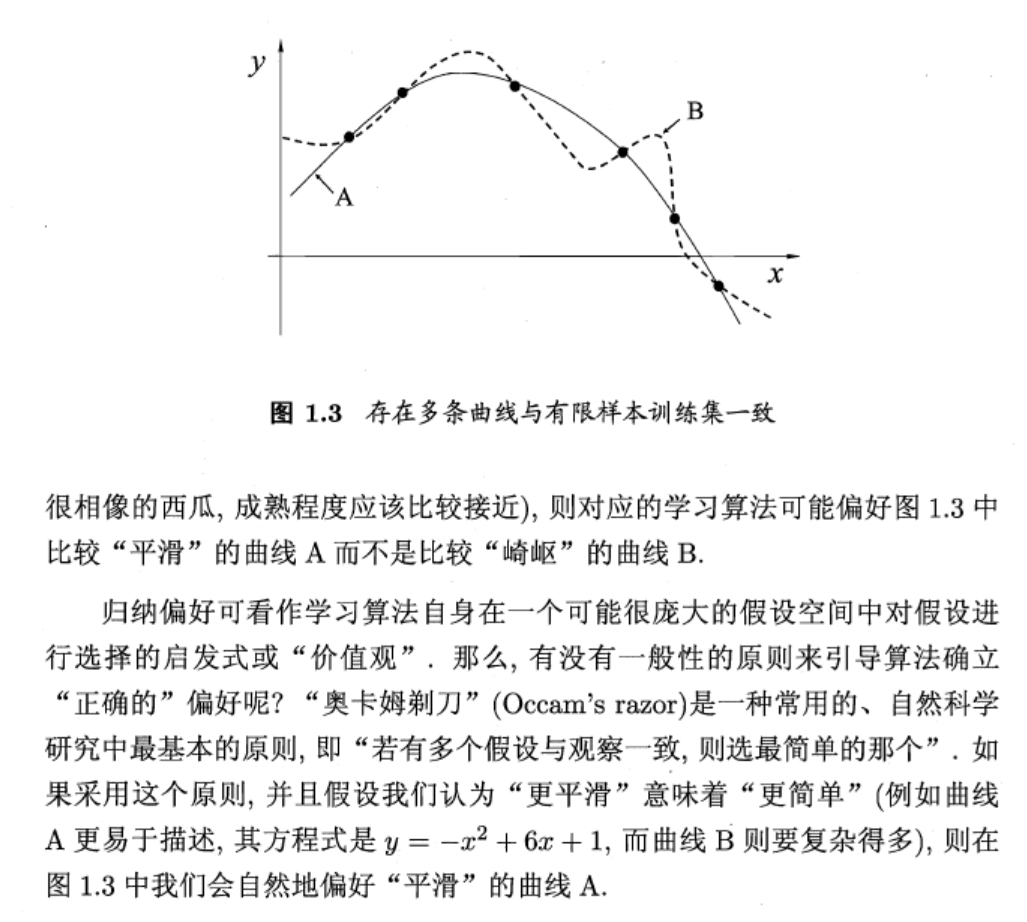
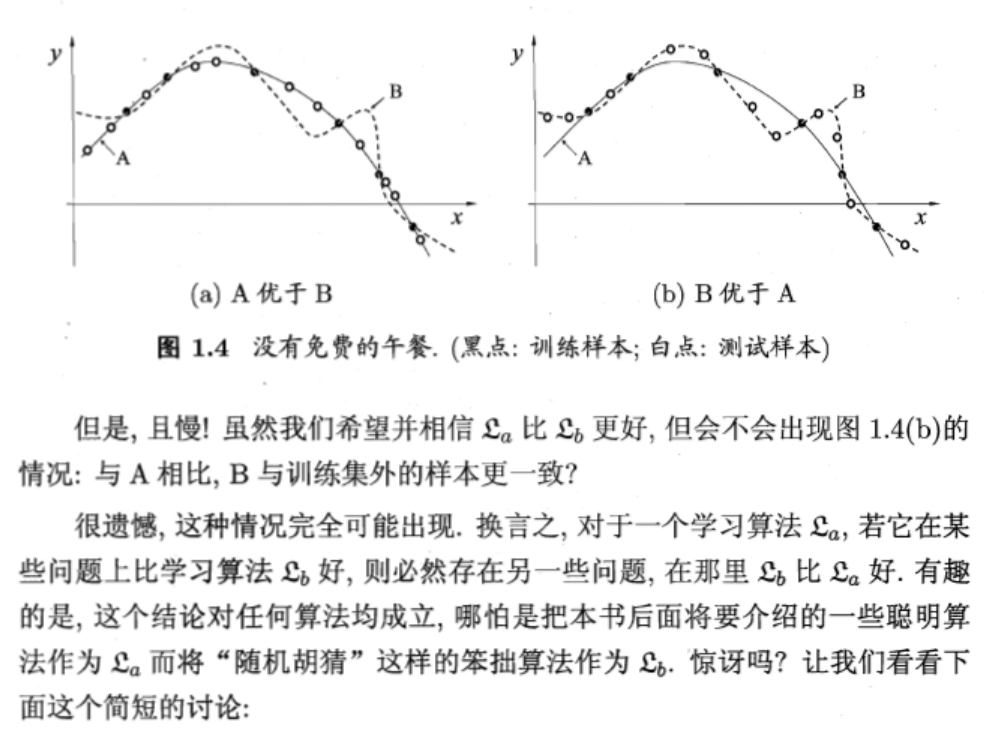
发展历程

机器学习是人工智能 artificial intelligence 研究发展到一定阶段的必然产物。

• 二十世纪五十年代到七十年代：推理期
• 二十世纪七十年代中期开始：知识期
• 二十世纪八十年代：机器学习

应用现状

在过去二十年中，人类收集、存储、传输、处理数据的能力取得了飞速提升，人类社会的各个角落都积累了大量数据，亟需有效地对数据进行分析利用的计算机算法，而机器学习恰顺应了大时代的迫切需求，因此该学科领域很自然地取得巨大发展、受到广泛关注。

2006年卡耐基梅隆大学宣告成立世界上第一个"机器学习系"。

大数据时代的三大关键技术：机器学习、云计算、众包 crowdsourcing。机器学习在大数据时代是必不可少的核心技术，道理很简单：收集、存储、传输、管理大数据的目的，是为了利用大数据，而如果没有机器学习技术分析数据，则利用无从谈起。

数据挖掘是从海量数据中发掘知识，这就必然涉及对海量数据的管理和分析。数据库领域的研究为数据挖掘提供数据管理技术，而机器学习和统计学的研究为数据挖掘提供分析技术。机器学习和数据库领域则是数据挖掘的两大支撑。

小结

1. 问题与基本术语

• 通过计算的手段，利用经验来改善系统自身的性能
• 有了数据
  • 数据集：100个西瓜
  • 样本：1个西瓜
  • 特征向量
    • 样本空间
    • 颜色，大小，敲起来的振幅
    • 维度
  • 属性：甜度
• 通过某种学习算法
  • 学习
  • 训练
• 得到模型
  • 分类
    • 二分类
      • Y正负
      • 瓜农眼中：这个瓜该不该摘，这个瓜熟没熟，这个瓜该不该卖
    • 多分类
      • Y大于2
      • 市场上要买哪种西瓜：黑美人，小地雷，特小凤
  • 回归
    • Y=R实数集
    • 某段时间内西瓜的价格，啥时候卖西瓜最合适
  • 聚类
    • 我们不知道要分几类，机器自己分
    • 每个组称为簇 cluster
• 进行预测
  • 测试
  • 测试样本
  • 泛化能力

模型评估与选择

经验误差与过拟合

评估方法

1. 留出法

2. 交叉验证法

3. 自助法

4. 调参与最终模型

线性模型

1. 基本形式

向量解释

当向量中的元素用分号“;”分隔时表示此向量为列向量，用逗号“,”分隔时表示为行向量。

2. 线性回归

上式也叫损失函数。

公式3.4解释

首先解释一下符号“arg min”，其中“arg”是“argument”（参数）的前三个字母，“min”是“minimum”（最小值）的前三个字母，该符号表示求使目标函数达到最小值的参数取值。例如式(3.4) 表示求出使目标函数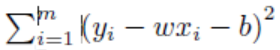达到最小值的参数取值(w∗, b∗)，注意目标函数是以(w, b) 为自变量的函数，(xi, yi) 均是已知常量，即训练集中的样本数据。

最小二乘法

基于均方误差最小化来进行模型求解的方法称为最小二乘法(least square method)。1801年意大利天文学家皮亚齐发现了1号小行星"谷神星"，但在跟踪观测了40天后，因谷神星转至太阳的背后，皮亚齐失去了谷神星的位置。许多天文学家试图重新找到谷神星，但都徒劳无获。这引起了伟大的德国数学家高斯(1777-1855)的注意，他发明了一种方法，根据皮亚齐的观测数据计算出了谷神星的轨道，后来德国天文学家奥伯斯在高斯预言的时间和星空领域重新找到了谷神星。1809年，高斯在他的著作《天体运动论》中发表了这种方法，即最小二乘法。

最小二乘法估计

公式3.5解释

在式(3.5) 左侧给出的凸函数的定义是最优化中的定义，与高等数学中的定义不同，本书也默认采用此种定义。由于一元线性回归可以看作是多元线性回归中元的个数为1 时的情形，所以此处暂不给出E(w,b) 是关于w 和b 的凸函数的证明。

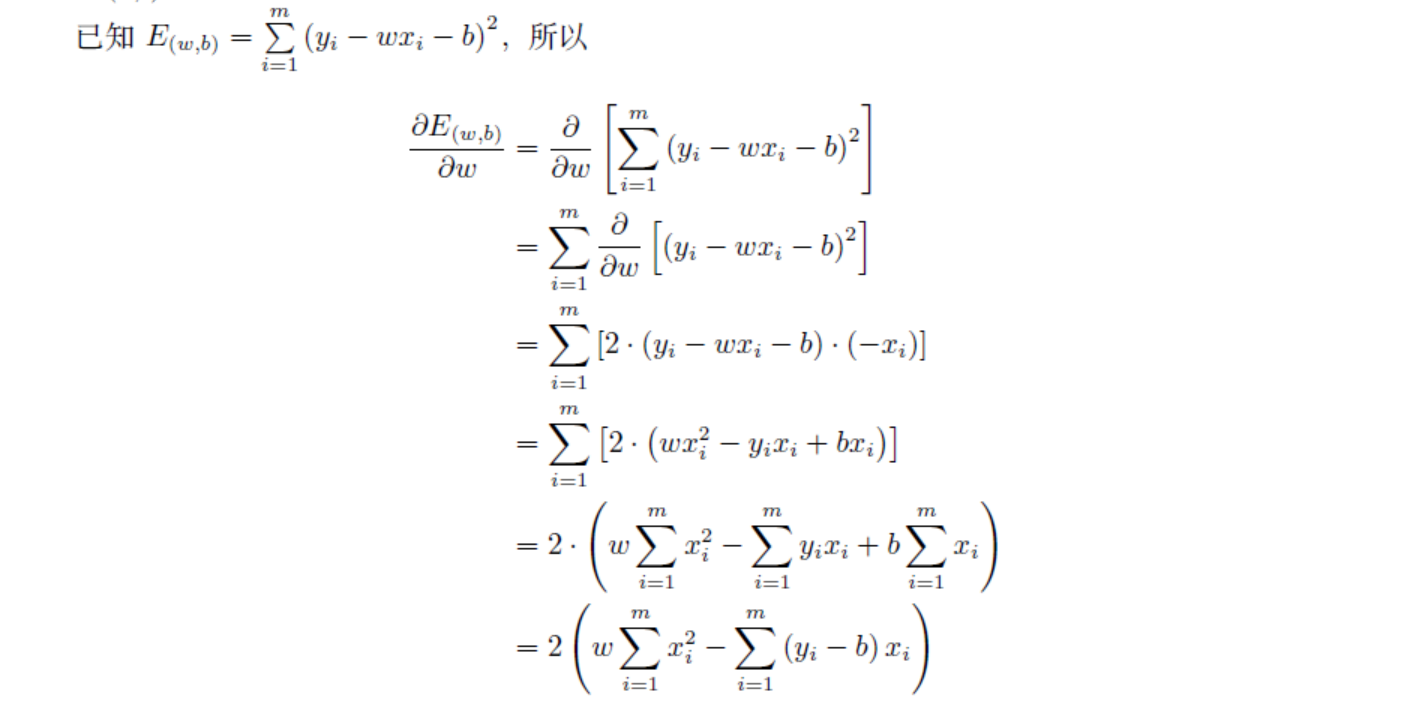
公式3.6解释

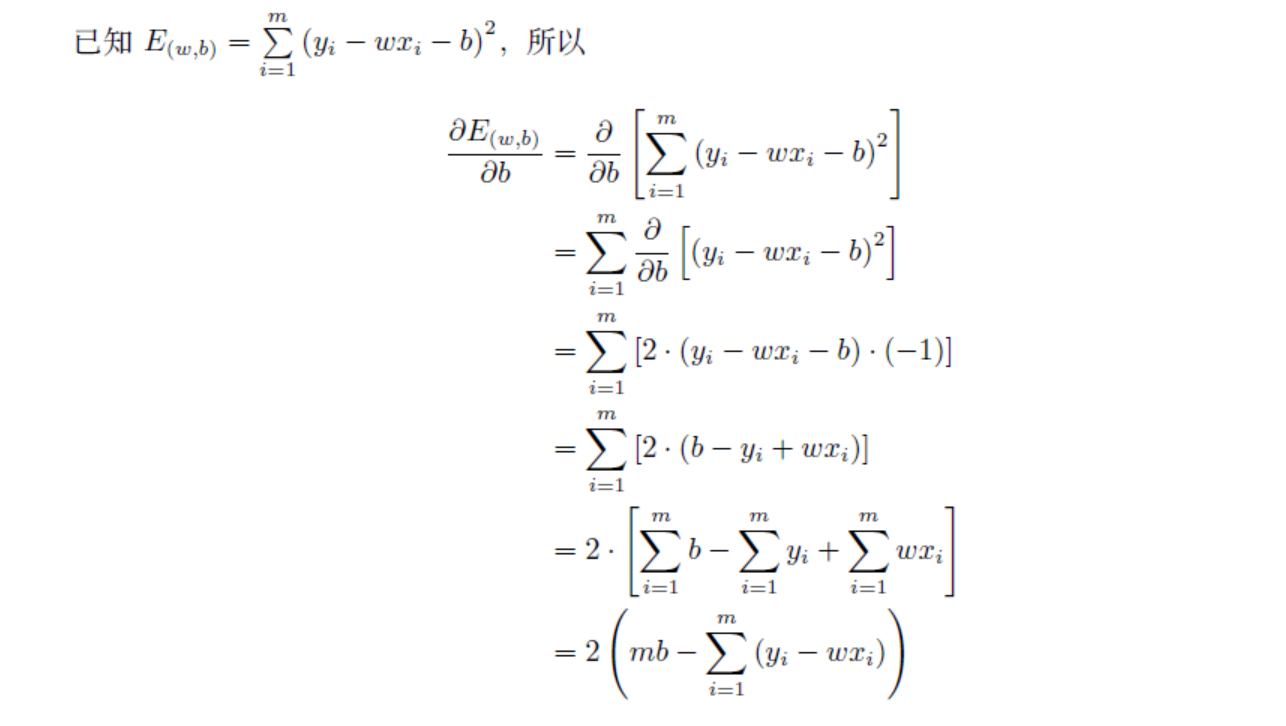
闭式解

“闭式解”或称为“解析解”。闭式解是指可以通过具体的表达式解出待解参数，例如可根据式(3.7) 直接解得w。机器学习算法很少有闭式解，线性回归是一个特例。

公式3.7解释

公式3.9解释

公式3.10解释

公式3.11解释

属性数值化

为了能进行数学运算，样本中的非数值类属性都需要进行数值化。对于存在“序”关系的属性，可通过连续化将其转化为带有相对大小关系的连续值；对于不存在“序”关系的属性，可根据属性取值将其拆解为多个属性，例如“瓜类”属性，可将其拆解为“是否是西瓜”、“是否是南瓜”、“是否是黄瓜”3 个属性，其中每个属性的取值为1 或0，1 表示“是”，0 表示“否”。具体地，假如现有3 个瓜类样本：x1 = (甜度= 高; 瓜类= 西瓜), x2 = (甜度= 中; 瓜类= 南瓜), x3 = (甜度= 低; 瓜类= 黄瓜)，其中“甜度”属性存在序关系，因此可将“高”、“中”、“低”转化为{1.0, 0.5, 0.0}，“瓜类”属性不存在序关系，则按照上述方法进行拆解，3 个瓜类样本数值化后的结果为：x1 = (1.0; 1; 0; 0), x1 = (0.5; 0; 1; 0), x1 = (0.0; 0; 0; 1)。

算法原理

极大似然估计

3. 对数几率回归

4. 线性判别分析

5. 多分类学习

现实中常遇到多分类学习任务。有些二分类学习方法可直接推广到多分类，但在更多情况下，我们是基于一些基本策略，利用二分类学习器来解决多分类问题。多分类学习的基本思路是"拆解法"，即将多分类任务拆为若干个二分类任务求解。具体来说，先对问题进行拆分，然后为拆出的每个二分类任务训练一个分类器，在测试时，对这些分类器的预测结果进行集成以获得最终的多分类结果。这里的关键是如何对多分类任务进行拆分，以及如何对多个分类器进行集成。

三种经典拆分策略："一对一 One vs. One 简称OvO"、"一对其余 One vs. Rest 简称OvR"和"多对多Many vs. Many 简称MvM"。

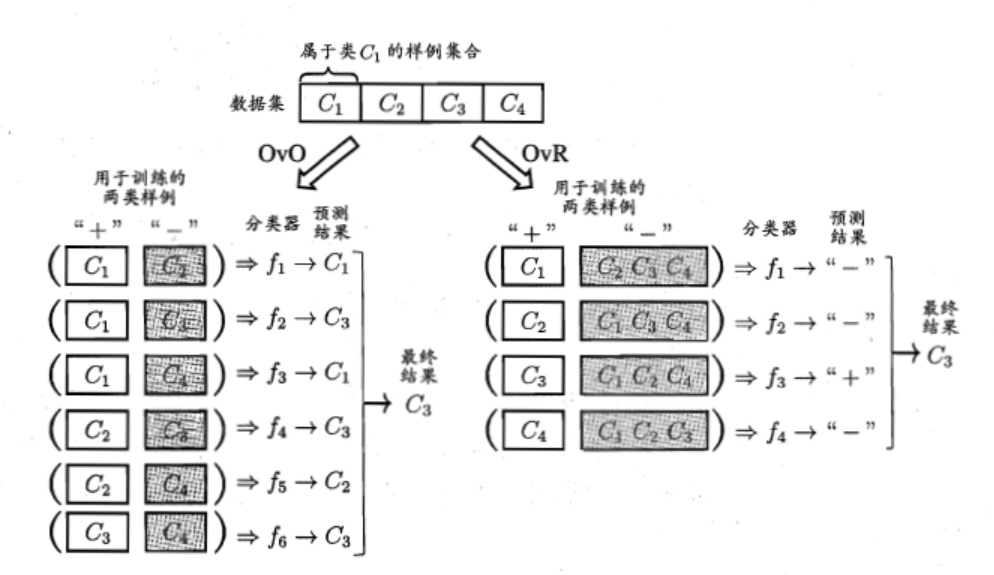
• OvO：将N个类别两两配对，从而产生N(N-1)/2个二分类任务。OvO将为区分类别Ci和Cj训练一个分类器，该分类器把数据集中的Ci类样例作为正例，Cj类样例作为反例。在测试阶段，新样本将同时提交给所有分类器，于是我们将得到N(N-1)/2个分类结果，最终结果可通过投票产生：即把被预测的最多的类别作为最终分类结果。
• OvR：每次将一个类的样例作为正例，所有其他类的样例作为反例来训练N个分类器。在测试时若仅有一个分类器预测为正类，则对应的类别标记作为最终分类结果。若有多个分类器预测为正类，则通常考虑各分类器的预测置信度，选择置信度最大的类别标记作为分类结果。

• MvM：每次将若干个类作为正类，若干个其他类作为反类。显然OvO和OvR是MvM的特例。MvM的正、反类构造必须有特殊的设计，不能随意选取。常用的MvM技术：纠错输出码 (Error Correcting Output Codes，简称ECOC)。ECOC[Diretterich and Bakiri，1995]是将编码的思想引入类别拆分，并尽可能在解码过程中具有容错性。ECOC工作过程主要有两个步骤：
  • 编码：对N个类别做M次划分，每次划分将一部分类别划分为正类，一部分划分为反类，从而形成一个二分类训练集。这样一共产生M个训练集，可以训练出M个分类器。
  • 解码：M个分类器分别对测试样本进行预测，这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较，返回其中距离最小的类别最为最终预测结果。

6. 类别不平衡问题

前面介绍的分类学习方法都有一个共同的基本假设，即不同类别的训练样例数目相当。如果不同类别的训练样例数目稍有差别，通常影响不大，但若差别很大，则会对学习过程造成困扰。例如有998个反例，只有2个正例，那么学习方法只需要返回一个永远将新样本预测为反例的学习器，就能达到99.8%的精度。然而这样的学习器往往没有价值，因为它不能预测出任何正例。

类别不平衡(class-imbalance)就是指分类任务中不同类别的训练样例数目差别很大的情况。下面假设正类样例较少，反类样例较多。

小结

• 基本形式
  • 问题描述
  • 函数形式
  • 向量形式
• 线性回归
  • 问题描述
  • 一元线性回归
  • 多元线性回归
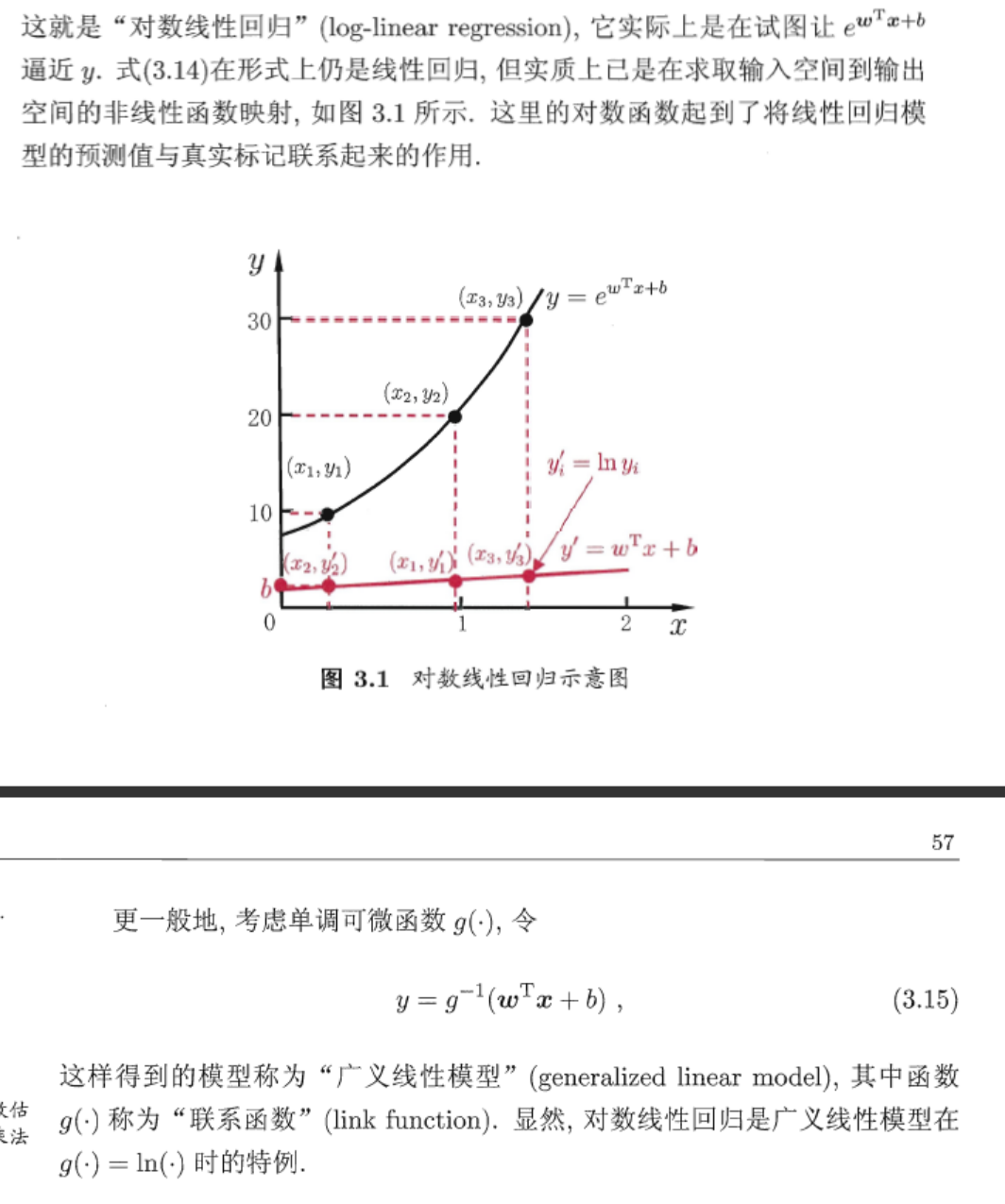
  • 对数线性回归
  • 广义线性回归
• 对数几率回归(逻辑回归)
• 线性判断分析
• 多分类学习
• 类别不平衡问题
• 梯度下降法

决策树

基本流程

决策树 (decision tree)是一种基本的分类与回归方法。以二分类任务为例，我们希望从给定训练数据集学得一个模型用以对新示例进行分类，这个把样本分类的任务，可看作对"当前样本属于正类吗"这个问题的"决策"或"判定"过程。

顾名思义，决策树是基于树结构来进行决策的，这恰是人类在面临决策问题时一种自然的处理机制。显然，决策过程的最终结论对应了我们所希望的判定结果，决策过程中提出的每个判定问题都是对某个属性的"测试"。每个测试的结果或是导出最终结论，或是导出进一步的判断问题，其考虑范围是在上次决策结果的限定范围之内。

一般的，一个决策树包含一个根结点、若干个内部结点和若干个叶结点。叶结点对应于决策结果，其他每个结点则对应于一个属性测试。每个结点包含的样本集合根据属性测试的结果被划分到子结点中。根结点包含样本全集。从根结点到每个叶结点的路径对应了一个判定测试序列。决策树学习的目的是为了产生一颗泛化能力强，即处理未见示例能力强的决策树，其基本流程遵循简单且直观的"分而治之"策略。

显然，决策树的生成是一个递归过程。在决策树基本算法中，有三种情形会导致递归返回：1.当前结点包含的样本全属于同一个类别，无需划分；2.当前属性集为空，或是所有样本在所有属性上取值相同，无法划分；3.当前结点包含的样本集合为空，不能划分。在第2种情形下，我们把当前结点标记为页结点，并将其类别设定为该结点所含样本最多的类别。在第3种情形下，同样把当前结点标记为叶结点，但将其类别设定为其父节点所含样本最多的类别。在第2种情形下是利用当前结点的后验分布，情形3则是把父节点的样本分布作为当前结点的先验分布。

划分选择

信息熵 information entrpoy 是度量样本集合纯度最常用的一种指标。