讲师曹建：北京大学软件与微电子学院

第一讲

本讲目标：学会神经网络计算过程，使用基于TF2原生代码搭建你的第一个的神经网络训练模型

• 当今人工智能主流方向——连接主义

• 前向传播

• 损失函数（初体会）

• 梯度下降（初体会）

• 学习率（初体会）

• 反向传播更新参数

• Tensorflow2 常用函数

人工智能：让机器具备人的思维和意识。

人工智能三学派

行为主义：基于控制论，构建感知-动作控制系统。（控制论，如平衡、行走、避障等自适应控制系统）

符号主义：基于算数逻辑表达式，求解问题时先把问题描述为表达式，再求解表达式。（可用公式描述、实现理性思维，如专家系统）

连接主义：仿生学，模仿神经元连接关系。（仿脑神经元连接，实现感性思维，如神经网络）

用计算机仿出神经网络连接关系，让计算机具备感性思维

准备数据：采集大量“特征/标签”数据

搭建网络：搭建神经网络结构

优化参数：训练网络获取最佳参数（反传）

应用网络：将网络保存为模型，输入新数据输出分类或预测结果（前传）

损失函数

损失函数（loss function）：预测值（y）与标准答案（y_）的差距。损失函数可以定量判断W、b的优劣，当损失函数输出最小时，参数W、b会出现最优值。

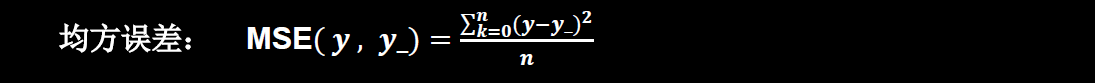
梯度下降

目的：想找到一组参数w和b，使得损失函数最小。

梯度：函数对各参数求偏导后的向量。函数梯度下降方向是函数减小方向。

梯度下降法：沿损失函数梯度下降的方向，寻找损失函数的最小值，得到最优参数的方法。

学习率

学习率（learning rate，lr）：当学习率设置的过小时，收敛过程将变得十分缓慢。而当学习率设置的过大时，梯度可能会在最小值附近来回震荡，甚至可能无法收敛。

反向传播

反向传播：从后向前，逐层求损失函数对每层神经元参数的偏导数，迭代更新所有参数。

tensorflow数据类型

• tf.int

  tf.int32
  

• tf.float

  tf.float32 
  
  tf.float64
  

• tf.bool

  tf.constant([True,False])
  

• tf.string

  tf.constant("Hello World!")
  

创建一个张量

import tensorflow as tf
import numpy as np

# 创建一个张量
a = tf.constant([1, 5], dtype=tf.int64)
print(a)
# tf.Tensor([1 5], shape=(2,), dtype=int64)
print(a.dtype)
# <dtype: 'int64'>
print(a.shape)
# (2,)

# 转换其他数据成张量
a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype=tf.int64)
print(a)
# [0 1 2 3 4]
print(b)
# tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64)

a = tf.zeros([2, 3])
b = tf.ones(4)
c = tf.fill([2, 2], 9)
print(a)
# tf.Tensor(
# [[0. 0. 0.]
#  [0. 0. 0.]], shape=(2, 3), dtype=float32)
print(b)
# tf.Tensor([1. 1. 1. 1.], shape=(4,), dtype=float32)
print(c)
# tf.Tensor(
# [[9 9]
#  [9 9]], shape=(2, 2), dtype=int32)

# 生成正态分布的随机数，默认均值为0，标准差为1
a = tf.random.normal([2, 2], mean=0.5, stddev=1)
print(a)
# tf.Tensor(
# [[ 1.775728    0.3096698 ]
#  [-0.10211772 -0.77820444]], shape=(2, 2), dtype=float32)

# 生成截断式正态分布的随机数
b = tf.random.truncated_normal([2, 2], mean=0.5, stddev=1)
print(b)
# tf.Tensor(
# [[ 1.2296319   0.45185208]
#  [ 0.27132237 -0.21660656]], shape=(2, 2), dtype=float32)

# 生成均匀分布随机数
c = tf.random.uniform([2, 2], minval=0, maxval=1)
print(c)
# tf.Tensor(
# [[0.96419454 0.98634803]
#  [0.1590271  0.8990524 ]], shape=(2, 2), dtype=float32)

常用函数

import tensorflow as tf

a = tf.constant([1., 2., 3.], dtype=tf.float64)
print(a)
# tf.Tensor([1. 2. 3.], shape=(3,), dtype=float64)

# 强制tensor转换为该数据类型
a = tf.cast(a, tf.int32)
print(a)
# tf.Tensor([1 2 3], shape=(3,), dtype=int32)
# 计算张量维度上元素的最小值
# 计算张量维度上元素的最大值
print(tf.reduce_min(a), tf.reduce_max(a))
# tf.Tensor(1, shape=(), dtype=int32) tf.Tensor(3, shape=(), dtype=int32)

# 计算张量沿着指定维度的平均值
a = tf.constant([[1, 2, 3], [2, 2, 3]])
print(a)
# tf.Tensor(
# [[1 2 3]
#  [2 2 3]], shape=(2, 3), dtype=int32)
print(tf.reduce_mean(a))
# tf.Tensor(2, shape=(), dtype=int32)

# 计算张量沿着指定维度的和
print(tf.reduce_sum(a, axis=1))
# tf.Tensor([6 7], shape=(2,), dtype=int32)

# 标记为可训练
w = tf.Variable(tf.random.normal([2, 2], mean=0, stddev=1))
print(w)
# array([[-1.2908813 ,  0.40013087],
#        [-0.30603158,  0.6309189 ]], dtype=float32)>

# 张量四则运算
a = tf.ones([1, 3])
b = tf.fill([1, 3], 3.)
print(a)
# tf.Tensor([[1. 1. 1.]], shape=(1, 3), dtype=float32)
print(b)
# tf.Tensor([[3. 3. 3.]], shape=(1, 3), dtype=float32)
print(tf.add(a, b))
# tf.Tensor([[4. 4. 4.]], shape=(1, 3), dtype=float32)
print(tf.subtract(a, b))
# tf.Tensor([[-2. -2. -2.]], shape=(1, 3), dtype=float32)
print(tf.multiply(a, b))
# tf.Tensor([[3. 3. 3.]], shape=(1, 3), dtype=float32)
print(tf.divide(b, a))
# tf.Tensor([[3. 3. 3.]], shape=(1, 3), dtype=float32)

a = tf.fill([1, 2], 3.)
print(a)

# 计算张量的次方
print(tf.pow(a, 3))
# tf.Tensor([[27. 27.]], shape=(1, 2), dtype=float32)
# 计算张量的平方
print(tf.square(a))
# tf.Tensor([[9. 9.]], shape=(1, 2), dtype=float32)
# 计算张量的开方
print(tf.sqrt(a))
# tf.Tensor([[1.7320508 1.7320508]], shape=(1, 2), dtype=float32)

a = tf.ones([3, 2])
b = tf.fill([2, 3], 3.)
# 实现两个矩阵相乘
print(tf.matmul(a, b))
# tf.Tensor(
# [[6. 6. 6.]
#  [6. 6. 6.]
#  [6. 6. 6.]], shape=(3, 3), dtype=float32)

# 加载数据集
features = tf.constant([12, 23, 10, 17])
labels = tf.constant([0, 1, 1, 0])
dataset = tf.data.Dataset.from_tensor_slices((features, labels))
print(dataset)
for element in dataset:
    print(element)
# <TensorSliceDataset shapes: ((), ()), types: (tf.int32, tf.int32)>
# (<tf.Tensor: shape=(), dtype=int32, numpy=12>, <tf.Tensor: shape=(), dtype=int32, numpy=0>)
# (<tf.Tensor: shape=(), dtype=int32, numpy=23>, <tf.Tensor: shape=(), dtype=int32, numpy=1>)
# (<tf.Tensor: shape=(), dtype=int32, numpy=10>, <tf.Tensor: shape=(), dtype=int32, numpy=1>)
# (<tf.Tensor: shape=(), dtype=int32, numpy=17>, <tf.Tensor: shape=(), dtype=int32, numpy=0>)

# with 结构记录计算过程，gradient求出张量的梯度
with tf.GradientTape() as tape:
    w = tf.Variable(tf.constant(3.))
    loss = tf.pow(w, 2)
grad = tape.gradient(loss, w)
print(grad)
# tf.Tensor(6.0, shape=(), dtype=float32)

# 遍历每个元素(列表，元组，字符串)，常在for循环中使用
for i, element in enumerate(['one', 'two', 'three']):
    print(i, element)
# 0 one
# 1 two
# 2 three

# n 分类的 n 个输出(y0,y1,y2,...,yn)通过softmax()函数，便符合概率分布了
y = tf.constant([1.01, 2.01, -0.66])
y_pro = tf.nn.softmax(y)
print('After softmax,y_pro is:', y_pro)
# After softmax,y_pro is: tf.Tensor([0.25598174 0.69583046 0.0481878 ], shape=(3,), dtype=float32)

# 调用assign_sub前，先用tf.Variable定义变量w为可训练(可自更新)
# 赋值操作，更新参数的值并返回
w = tf.Variable(4)
w.assign_sub(1)
print(w)
# <tf.Variable 'Variable:0' shape=() dtype=int32, numpy=3>

# 返回张量沿指定维度最大值的索引
test = np.array([[1, 2, 3], [2, 3, 4], [5, 4, 3], [8, 7, 2]])
print(test)
print(tf.argmax(test, axis=0))
print(tf.argmax(test, axis=1))
# [[1 2 3]
#  [2 3 4]
#  [5 4 3]
#  [8 7 2]]
# tf.Tensor([3 3 1], shape=(3,), dtype=int64)
# tf.Tensor([2 2 0 0], shape=(4,), dtype=int64)

tf.where

# 条件语句真返回A，条件语句为假返回B
a = tf.constant([1, 2, 3, 1, 1])
b = tf.constant([0, 1, 3, 4, 5])
c = tf.where(tf.greater(a, b), a, b)  # 若a>b，返回a对应位置的元素，否则返回b对应位置的元素
print("c:", c)
# c: tf.Tensor([1 2 3 4 5], shape=(5,), dtype=int32)

tf.one_hot

# 将待转换数据，转换为 one-hot形式的数据输出
classes = 3
labels = tf.constant([1, 0, 2])  # 输入的元素最小值为0，最大值为2
output = tf.one_hot(labels, depth=classes)
print(output)
# tf.Tensor(
# [[0. 1. 0.]
#  [1. 0. 0.]
#  [0. 0. 1.]], shape=(3, 3), dtype=float32)

one_hot

一句话概括：one hot编码是将类别变量转换为机器学习算法易于利用的一种形式的过程。

一个特征变成了n个特征，比如编码之前它属于玫瑰，编码之后它具有3个特征：不是百合，不是水仙，是玫瑰。所以就当成很多特征，直接输入神经网络就可以了。